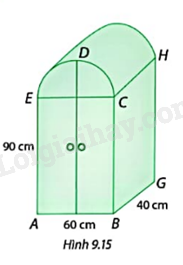
Giải bài tập 9.5 trang 68 SGK Toán 9 tập 2 - Cùng khám pháHình 9.15 là một tủ chứa đồ. Biết cung CDE là nửa đường tròn. a) Tính thể tích của tủ đồ. b) Người ta muốn sơn tất cả các mặt ngoài của tủ (kể cả đáy). Hỏi diện tích cần sơn là bao nhiêu mét vuông (làm tròn kết quả đến hàng phần mười)? Đề bài Hình 9.15 là một tủ chứa đồ. Biết cung CDE là nửa đường tròn. a) Tính thể tích của tủ đồ. b) Người ta muốn sơn tất cả các mặt ngoài của tủ (kể cả đáy). Hỏi diện tích cần sơn là bao nhiêu mét vuông (làm tròn kết quả đến hàng phần mười)?
Phương pháp giải - Xem chi tiết Dựa vào thể tích hình trụ: V = \(\pi {r^2}h\) (với r là bán kính đáy và h là chiều cao hình trụ). Dựa vào: Diện tích xung quanh hình hộp chữ nhật Sxq = (a + b).2 (với a,b lần lượt là chiều dài, chiều rộng), diện tích xung quanh hình trụ \({S_{xq}} = 2\pi rh\) (với r là bán kính đáy và h là chiều cao hình trụ). Lời giải chi tiết a) Thể tích phần thân tủ dưới dạng hình hộp chữ nhật là 90.60.40 = 216000 (cm3) Thể tích phần thân tủ trên là: \(\frac{{\pi {{.30}^2}.40}}{2} = 18000\pi \) (cm3) Vậy thể tích của tủ đồ là: 216000 + \(18000\pi \) = 272548,7 (cm3). b) Diện tích xung quanh phần thân tủ dưới dạng hình hộp chữ nhật là: Sxq + Sđáy = (40 + 60).2.90 + 40.60 = 20400 (cm2) Diện tích xung quanh phần thân tủ trên là: \(\frac{{2\pi .30.40}}{2} = 1200\pi \) (cm2) Vậy diện tích cần sơn là: 20400 + 1200\(\pi \)\( \approx \)24169,9 cm2.  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
