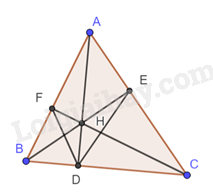
Giải bài tập 7.12 trang 38 SGK Toán 9 tập 2 - Cùng khám phá

Đề bài

Cho tam giác nhọn ABC có AD, BE, CF là đường cao và H là trực tâm. Chứng minh rằng

a) Tứ giác AEHF, BDHF và CDHE là các tứ giác nội tiếp

b) DA là đường phân giác của góc FDE.

Lời giải chi tiết

a) Ta có $\widehat {AEH} = \widehat {AFH} = {90^o}$ (Do CF và BE là đường cao)

suy ra AEHF là tứ giác nội tiếp.

Chứng minh tương tự BDHF và CDHE là các tứ giác nội tiếp

b) Theo phần a ta có BDHF nội tiếp nên $\widehat {ABE} = \widehat {FDA}$

DHEC nội tiếp nên $\widehat {ADE} = \widehat {FCA}$.

Lại có $\widehat {ABE} = \widehat {FCA}$ (cùng phụ $\widehat {BAC}$)

Suy ra $\widehat {FDA} = \widehat {ADE}$ hay AD là đường phân giác của góc FDE.