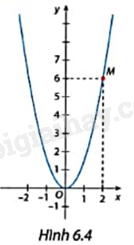
Giải bài tập 6.3 trang 5 SGK Toán 9 tập 2 - Cùng khám pháCho hàm số y = ax2 có đồ thị là đường parabol như Hình 6.4 a) Tìm hệ số a. b) Tìm tung độ của điểm thuộc đồ thị có hoành độ bằng -1. c) Tìm các điểm thuộc đồ thị có tung độ bằng \(\frac{2}{3}\). Đề bài Cho hàm số y = ax2 có đồ thị là đường parabol như Hình 6.4 a) Tìm hệ số a. b) Tìm tung độ của điểm thuộc đồ thị có hoành độ bằng -1. c) Tìm các điểm thuộc đồ thị có tung độ bằng \(\frac{2}{3}\).
Phương pháp giải - Xem chi tiết Thay toạ độ điểm M(2;6) vào y = ax2 để tìm a. Thay x = -1 để tìm y. Thay y = \(\frac{2}{3}\) để tìm x. Lời giải chi tiết a) Thay toạ độ điểm M(2;6) vào y = ax2 ta có: 6 = a.22 a = \(\frac{3}{2}\) b) Thay x = -1 vào y = \(\frac{3}{2}\)x2 ta được y = \( - \frac{3}{2}{( - 1)^2} = - \frac{3}{2}\). Điểm cần tìm là \(\left( { - 1; - \frac{3}{2}} \right)\). c) Thay y = \(\frac{2}{3}\) vào y = \(\frac{3}{2}\)x2 ta được \(\begin{array}{l}\frac{2}{3} = \frac{3}{2}{x^2}\\{x^2} = \frac{4}{9}\\\left[ {\begin{array}{*{20}{c}}{x = \frac{2}{3}}\\{x = - \frac{2}{3}}\end{array}} \right.\end{array}\) Điểm cần tìm là \(\left( {\frac{2}{3};\frac{2}{3}} \right);\left( { - \frac{2}{3};\frac{2}{3}} \right)\).
|