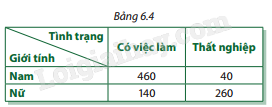
Giải bài tập 6.11 trang 105 SGK Toán 12 tập 2 - Cùng khám pháTrong một cuộc khảo sát tình trạng công việc trên 900 người đã có bằng tốt nghiệp trung học phổ thông ở một địa phương cho cả nam lẫn nữ, người ta thu được số liệu như Bảng 6.4. Đề bài Trong một cuộc khảo sát tình trạng công việc trên 900 người đã có bằng tốt nghiệp trung học phổ thông ở một địa phương cho cả nam lẫn nữ, người ta thu được số liệu như Bảng 6.4.
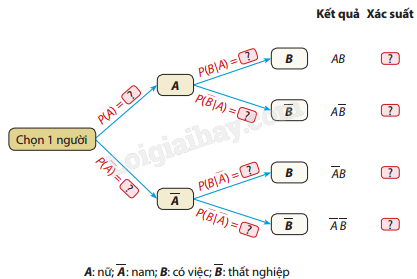
Chọn ngẫu nhiên một người trong nhóm này. Gọi A là biến cố "Người được chọn là nữ", B là biến cố "Người được chọn có việc làm". a) Vẽ lại sơ đồ hình cây sau đây và hoàn thành kết quả ở các ô ?
b) Tính xác suất để chọn được một người có việc làm. c) Biết rằng đã chọn được một người có việc làm, tính xác suất để người này là nữ. Phương pháp giải - Xem chi tiết Xác định các xác suất và sử dụng các công thức sau: - Xác suất có điều kiện: \(P(A|B) = \frac{{P(AB)}}{{P(B)}},\quad P(B|A) = \frac{{P(AB)}}{{P(A)}}\) - Xác suất của phần bù: \(P(\bar A) = 1 - P(A)\) - Xác suất toàn phần: \(P(B) = P(B|A) \cdot P(A) + P(B|\bar A) \cdot P(\bar A)\) Lời giải chi tiết a) Các xác suất là: * \(P(A) = \frac{{400}}{{900}} \approx 0,444\) * \(P(\bar A) = 1 - P(A) = 1 - 0,444 = 0,556\) * \(P(B|A) = \frac{{140}}{{400}} = 0,35\) * \(P(\bar B|A) = \frac{{260}}{{400}} = 0,65\) * \(P(B|\bar A) = \frac{{460}}{{500}} = 0,92\) * \(P(\bar B|\bar A) = \frac{{40}}{{500}} = 0,08\) * \(P(AB) = \frac{{140}}{{900}} \approx 0,156\) * \(P(A|B) = \frac{{P(AB)}}{{P(B)}}\): + \(P(B) = P(AB) + P(\bar AB)\): \(P(B) = \frac{{140}}{{900}} + \frac{{460}}{{900}} = \frac{{600}}{{900}} = 0,667\) + \(P(A|B) = \frac{{\frac{{140}}{{900}}}}{{0,667}} \approx 0,21\) * \(P(\bar AB) = \frac{{460}}{{900}} \approx 0,511\) * \(P(\bar A\bar B) = \frac{{40}}{{900}} \approx 0,044\) b) Xác suất để chọn được một người có việc làm: \(P(B) = 0,667{\mkern 1mu} (66,7\% ).\) c) Xác suất để người có việc làm là nữ: \(P(A|B) \approx 0,234{\mkern 1mu} (23,4\% ).\)
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM; 70+ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
|