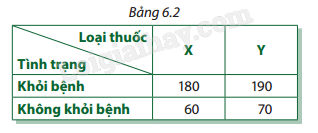
Giải bài tập 6.1 trang 96 SGK Toán 12 tập 2 - Cùng khám pháMột phòng nghiên cứu dược học cho 500 người bị bệnh H dùng hai loại thuốc X, Y để điều trị. Một số người được điều trị bằng thuốc X và số người còn lại được điều trị bằng thuốc Y. Kết quả nghiên cứu được trình bày ở Bảng 6.2. Đề bài Một phòng nghiên cứu dược học cho 500 người bị bệnh H dùng hai loại thuốc X, Y để điều trị. Một số người được điều trị bằng thuốc X và số người còn lại được điều trị bằng thuốc Y. Kết quả nghiên cứu được trình bày ở Bảng 6.2.
Chọn ngẫu nhiên một người trong số này. Gọi A là biến cố "Người được chọn khỏi bệnh", B là biến cố "Người được chọn điều trị bằng thuốc X", C là biến cố "Người được chọn điều trị bằng thuốc Y". a) Tính và giải thích ý nghĩa của \(P(A|B)\) và \(P(A|C)\). b) Có thể nói loại thuốc nào có hiệu quả hơn trong việc điều trị bệnh H? Phương pháp giải - Xem chi tiết a) Sử dụng công thức xác suất có điều kiện: \(P(A|B) = \frac{{P(AB)}}{{P(B)}}\) . Tính \(P(A|B)\) và \(P(A|C)\) từ dữ liệu trong bảng. b) So sánh \(P(A|B)\) và \(P(A|C)\) để đưa ra kết luận. Lời giải chi tiết a) Tính \(P(A|B)\) và \(P(A|C)\): \(P(A|B) = \frac{{P(AB)}}{{P(B)}} = \frac{{180}}{{180 + 60}} = \frac{3}{4} = 0,75\) (xác suất chọn được người điều trị bằng thuốc X khỏi bệnh) \(P(A|C) = \frac{{P(AC)}}{{P(C)}} = \frac{{190}}{{190 + 70}} = \frac{{19}}{{26}} \approx 0,73\) (xác suất chọn được người điều trị bằng thuốc Y khỏi bệnh) b) So sánh \(P(A|B)\) và \(P(A|C)\): Vì \(P(A|B) > P(A|C)\), nên có thể kết luận rằng thuốc X có hiệu quả hơn thuốc Y trong việc điều trị bệnh H.
|