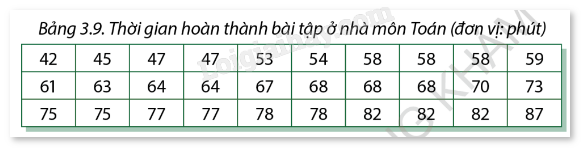
Giải bài tập 3.1 trang 94 SGK Toán 12 tập 1 - Cùng khám pháDưới đây là kết quả điều tra thời gian hoàn thành bài tập ở nhà môn Toán của 30 học sinh lớp 9: Đề bài Dưới đây là kết quả điều tra thời gian hoàn thành bài tập ở nhà môn Toán của 30 học sinh lớp 9:
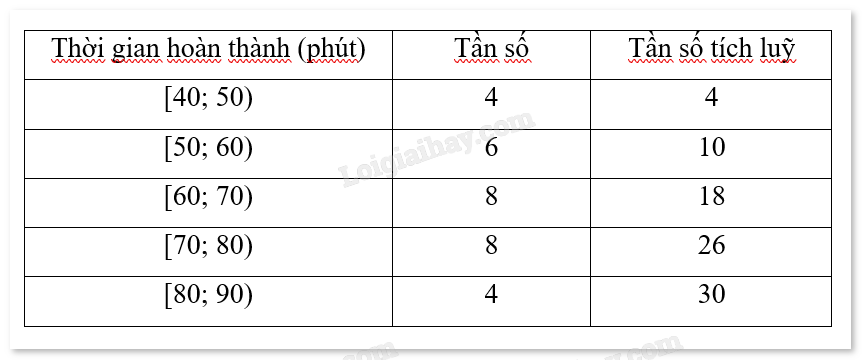
a) Tìm trung bình, các tứ phân vị và khoảng tứ phân vị của mẫu số liệu đã cho. b) Lập mẫu số liệu ghép nhóm với các nhóm ghép có độ dài bằng 10 và nhóm đầu tiên là [40;50). c) Tìm trung bình, khoảng biến thiên, các tứ phân vị và khoảng tứ phân vị của mẫu số liệu ghép nhóm lập ở câu b. d) So sánh các kết quả tìm được ở câu a và c. Giải thích vì sao có sự khác biệt. Phương pháp giải - Xem chi tiết a) Sắp xếp dãy số liệu theo thứ tự tăng dần. Tìm trung bình: Tính tổng các giá trị rồi chia cho số lượng phần tử. Tứ phân vị: - \({Q_1}\) là trung vị của nửa dưới (25% đầu). - \({Q_2}\) là trung vị của toàn bộ dữ liệu (tức là trung vị của dãy số). - \({Q_3}\)là trung vị của nửa trên (75%). Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1}\) b) Nhóm các giá trị từ 40-50, 50-60,... và đếm số lượng giá trị trong mỗi nhóm. c) Tìm trung bình: Tìm trung điểm của mỗi nhóm và nhân trung điểm đó với tần số tương ứng. Khoảng biến thiên: R bằng đầu mút phải của nhóm ghép cuối trừ đầu mút trái của nhóm ghép đầu tiên. Tứ phân vị: Sử dụng công thức \({Q_x} = L + \left( {\frac{{{n_x} - F}}{f}} \right) \times h\) Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1}\) d) So sánh sự khác biệt giữa trung bình, khoảng tứ phân vị, và các tứ phân vị. Lời giải chi tiết a) - Sắp xếp số liệu: 42, 45, 47, 47, 53, 54, 58, 58, 58, 59, 61, 63, 64, 64, 67, 68, 68, 68, 70, 73, 75, 75, 77, 77, 78, 78, 82, 82, 82, 87. - Tìm trung bình: \(\frac{{42 + 45 + 47 + ... + 82 + 82 + 87}}{{30}} = 66\) - Tứ phân vị: Vì mẫu số liệu có n = 2k nên: \({Q_2} = \frac{1}{2}\left( {{x_k} + {x_{k + 1}}} \right) = \frac{1}{2}\left( {67 + 68} \right) = 67,5\) \({Q_1} = \frac{1}{2}\left( {58 + 58} \right) = 58\) \({Q_3} = \frac{1}{2}\left( {77 + 77} \right) = 77\) - Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1} = 77 - 58 = 19\) b)
c) Tính trung bình: \(\frac{{45.4 + 55.6 + 65.8 + 75.8 + 85.4}}{{30}} = 66,87\)\(\) Khoản biến thiên: R = 90 – 40 = 50 Tứ phân vị: \({Q_1} = 50 + \frac{{7,5 - 4}}{6}.10 = 55,84\) \({Q_2} = 60 + \frac{{15 - 10}}{8}.10 = 66,25\) \({Q_3} = 70 + \frac{{22,5 - 18}}{8}.10 = 75,625\) Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1} = 75,625 - 55,84 = 19,785\) d) Có thể thấy các kết quả tìm được ở câu a và câu c có sự chênh lệch nhưng không quá nhiều. Sự khác biệt trong các kết quả tính toán giữa câu 3.1(a) và 3.1(c) là do quá trình nhóm dữ liệu làm mất đi chi tiết cụ thể của các giá trị trong dãy số liệu gốc, dẫn đến sự chênh lệch trong việc tính toán các giá trị thống kê.
|