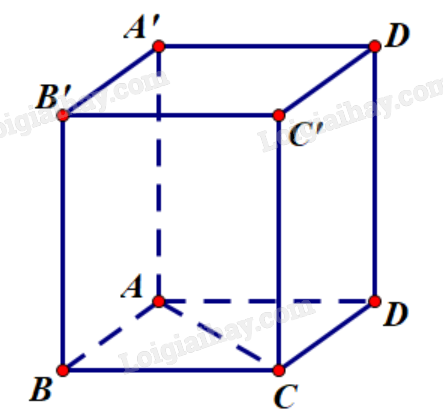
Giải bài tập 2.10 trang 59 SGK Toán 12 tập 1 - Kết nối tri thứcCho hình lăng trụ tứ giác đều ABCD.A’B’C’D’ có độ dài mỗi cạnh đáy bằng 1 và độ dài mỗi cạnh bên bằng 2. Hãy tính góc giữa các cặp vectơ sau đây và tính tích vô hướng của mỗi cặp vectơ đó: a) (overrightarrow {AA'} ) và (overrightarrow {C'C;} ) b) (overrightarrow {AA'} ) và (overrightarrow {BC;} ) c) (overrightarrow {AC} ) và (overrightarrow {B'A'} ). Tổng hợp đề thi học kì 2 lớp 12 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Hoá - Sinh - Sử - Địa Đề bài Cho hình lăng trụ tứ giác đều ABCD.A’B’C’D’ có độ dài mỗi cạnh đáy bằng 1 và độ dài mỗi cạnh bên bằng 2. Hãy tính góc giữa các cặp vectơ sau đây và tính tích vô hướng của mỗi cặp vectơ đó: Phương pháp giải - Xem chi tiết + Sử dụng kiến thức về góc giữa hai vectơ trong không gian để tính: Trong không gian, cho hai vectơ \(\overrightarrow a \), \(\overrightarrow b \) khác \(\overrightarrow 0 \). Lấy một điểm O bất kì và gọi A, B là hai điểm sao cho \(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b \). Khi đó, góc \(\widehat {AOB}\left( {{0^0} \le \widehat {AOB} \le {{180}^0}} \right)\) được gọi là góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \), kí hiệu là \(\left( {\overrightarrow a ,\overrightarrow b } \right)\). + Sử dụng kiến thức về công thức xác định tích vô hướng của hai vectơ trong không gian để tính: Trong không gian, cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) đều khác \(\overrightarrow 0 \). Tích vô hướng của hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) là một số, kí hiệu là \(\overrightarrow a \cdot \overrightarrow b \), được xác định bởi công thức sau: \(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \cos \left( {\overrightarrow a ,\overrightarrow b } \right)\). Lời giải chi tiết
a) Vì AA’ // CC’ nên hai vectơ \(\overrightarrow {AA'} \) và \(\overrightarrow {C'C} \) ngược hướng nhau. Suy ra, \(\left( {\overrightarrow {AA'} ,\overrightarrow {C'C} } \right) = {180^0}\). Do đó, \(\overrightarrow {AA'} .\overrightarrow {C'C} = \left| {\overrightarrow {AA'} } \right|.\left| {\overrightarrow {C'C} } \right|.\cos \left( {\overrightarrow {AA'} ,\overrightarrow {C'C} } \right) = 2.2.\cos {180^o} = - 4\). b) Vì A’ADD’ là hình chữ nhật nên \(\widehat {A'AD} = {90^o}\). Vì ABCD là hình vuông nên \(\overrightarrow {BC} = \overrightarrow {AD} \). Do đó, \(\left( {\overrightarrow {AA'} ,\overrightarrow {BC} } \right) = \left( {\overrightarrow {AA'} ,\overrightarrow {AD} } \right) = \widehat {A'AD} = {90^o}\). Ta có: \(\overrightarrow {AA'} .\overrightarrow {BC} = \overrightarrow {AA'} .\overrightarrow {AD} = \left| {\overrightarrow {AA'} } \right|.\left| {\overrightarrow {AD} } \right|.\cos \left( {\overrightarrow {AA'} ,\overrightarrow {AD} } \right) = 2.1.\cos {90^o} = 0\). c) Vì A’ABB’ là hình chữ nhật nên \(\overrightarrow {B'A'} = \overrightarrow {BA} \). Vì ABCD là hình vuông nên \(\widehat {CAB} = {45^o}\) và \(AC = \sqrt 2 \). Ta có: \(\overrightarrow {AC} .\overrightarrow {B'A'} = - \overrightarrow {AC} .\overrightarrow {AB} = - \left| {\overrightarrow {AC} } \right|.\left| {\overrightarrow {AB} } \right|.\cos \left( {\overrightarrow {AC} ,\overrightarrow {AB} } \right) = - \sqrt 2 .1.\cos {45^0} = - 1\). Suy ra \(\cos \left( {\overrightarrow {AC} ,\overrightarrow {B'A'} } \right) = \frac{{\overrightarrow {AC} .\overrightarrow {B'A'} }}{{AC.B'A'}} = \frac{{ - 1}}{{\sqrt 2 .1}} = {135^o}\).
|