Giải bài tập 1.40 trang 43 SGK Toán 12 tập 1 - Kết nối tri thức

Đề bài

Xét chiều biến thiên và tìm các cực trị (nếu có) của các hàm số sau:
a) \(y = {x^3} - 3{x^2} + 3x - 1\);
b) \(y = {x^4} - 2{x^2} - 1\);
c) \(y = \frac{{2x - 1}}{{3x + 1}}\);
d) \(y = \frac{{{x^2} + 2x + 2}}{{x + 1}}\).

Lời giải chi tiết

a) Tập xác định: \(D = \mathbb{R}\).

Ta có: \(y' = 3{x^2} - 6x + 3 = 3{\left( {x - 1} \right)^2},y' = 0 \Leftrightarrow x = 1\)

Lập bảng biến thiên của hàm số:

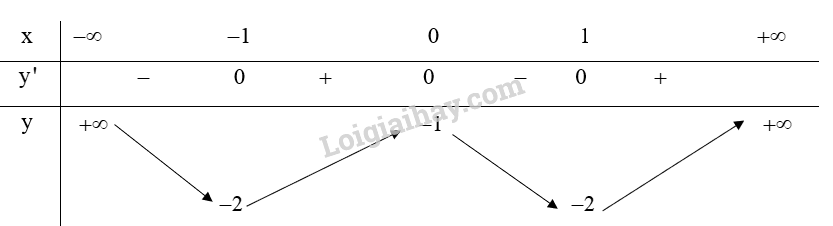
Hàm số \(y = {x^3} - 3{x^2} + 3x - 1\) đồng biến trên R.

Hàm số \(y = {x^3} - 3{x^2} + 3x - 1\) không có cực trị.

b) Tập xác định của hàm số là \(D = \mathbb{R}\).

Ta có: \(y' = 4{x^3} - 4x,y' = 0 \Leftrightarrow 4{x^3} - 4x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x =  \pm 1\end{array} \right.\)

Bảng biến thiên:

 

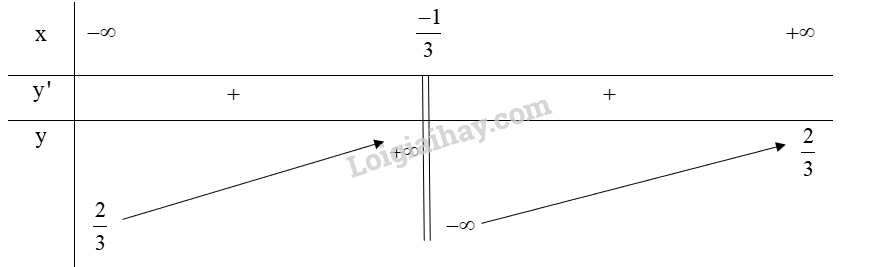
 Từ bảng biến thiên ta có:

Hàm số \(y = {x^4} - 2{x^2} - 1\) đồng biến trên khoảng \(\left( { - 1;0} \right)\) và \(\left( {1; + \infty } \right)\).

Hàm số \(y = {x^4} - 2{x^2} - 1\) nghịch biến trên khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {0;1} \right)\).

Hàm số \(y = {x^4} - 2{x^2} - 1\) đạt cực đại tại \(x = 0\) và .

Hàm số \(y = {x^4} - 2{x^2} - 1\) đạt cực tiểu tại \(x =  \pm 1\) và \({y_{CT}} =  - 2\).

c) Tập xác định: \(D = \mathbb{R}\backslash \left\{ { - \frac{1}{3}} \right\}\).

Ta có: \(y' = \frac{{2\left( {3x + 1} \right) - 3\left( {2x - 1} \right)}}{{{{\left( {3x + 1} \right)}^2}}} = \frac{5}{{{{\left( {3x + 1} \right)}^2}}} > 0\;\forall x \ne \frac{{ - 1}}{3}\)

Lập bảng biến thiên của hàm số:

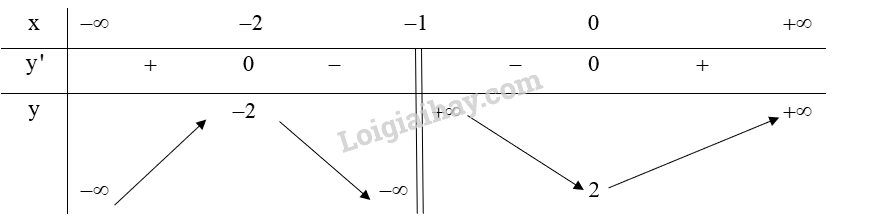
Từ bảng biến thiên ta có:

Hàm số \(y = \frac{{2x - 1}}{{3x + 1}}\) đồng biến trên \(\left( { - \infty ;\frac{{ - 1}}{3}} \right)\) và \(\left( {\frac{{ - 1}}{3}; + \infty } \right)\).

Hàm số không có cực trị.

d) Tập xác định: \(D = \mathbb{R}\backslash \left\{ { - 1} \right\}\).

Ta có: \(y' = \frac{{\left( {2x + 2} \right)\left( {x + 1} \right) - \left( {{x^2} + 2x + 2} \right)}}{{{{\left( {x + 1} \right)}^2}}} = \frac{{{x^2} + 2x}}{{{{\left( {x + 1} \right)}^2}}}\)

\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x =  - 2\end{array} \right.\) (thỏa mãn)

Lập bảng biến thiên của hàm số:

Từ bảng biến thiên ta có:

Hàm số \(y = \frac{{{x^2} + 2x + 2}}{{x + 1}}\) đồng biến trên khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( {0; + \infty } \right)\).

Hàm số \(y = \frac{{{x^2} + 2x + 2}}{{x + 1}}\) nghịch biến trên khoảng \(\left( { - 2; - 1} \right)\) và \(\left( { - 1;0} \right)\).

Hàm số \(y = \frac{{{x^2} + 2x + 2}}{{x + 1}}\) đạt cực đại tại \(x =  - 2\) và \({y_{CĐ}} = -2\).

Hàm số \(y = \frac{{{x^2} + 2x + 2}}{{x + 1}}\) đạt cực tiểu tại \(x = 0\) và \({y_{CT}} = 2\).