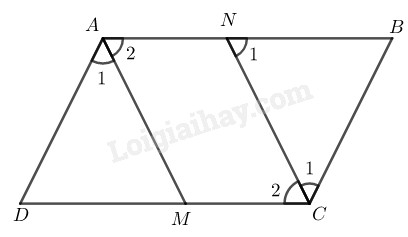
Bài 75 trang 89 SBT toán 8 tập 1Giải bài 75 trang 89 sách bài tập toán 8. Chứng minh rằng AMCN là hình bình hành. Đề bài Cho hình bình hành \(ABCD.\) Tia phân giác của góc \(A\) cắt \(CD\) ở \(M.\) Tia phân giác của góc \(C\) cắt \(AB\) ở \(N.\) Chứng minh rằng \(AMCN\) là hình bình hành. Phương pháp giải - Xem chi tiết Sử dụng kiến thức: Trong hình bình hành, hai góc đối bằng nhau. Dấu hiệu nhận biết: Tứ giác có các cạnh đối song song là hình bình hành. Lời giải chi tiết
Vì ABCD là hình bình hành nên \(\widehat A = \widehat C\) (tính chất hình bình hành) \( \displaystyle {\widehat A_2} = {1 \over 2}\widehat A\) (do AM là tia phân giác của góc BAD) \(\displaystyle {\widehat C_2} = {1 \over 2}\widehat C \) (do CN là tia phân giác của góc BCD) Suy ra: \(\widehat A_2=\widehat C_2\) (vì \(\widehat A = \widehat C)\) Lại có \(AB // CD\;\;\) (do ABCD là hình bình hành) Nên \(AN // CM \;\;(1)\) Mà \({\widehat N_1} = {\widehat C_2}\) (so le trong) Suy ra: \({\widehat A_2} = {\widehat N_1}\) \(⇒ AM // CN \) ( vì có các cặp góc ở vị trí đồng vị bằng nhau) \((2)\) Từ \((1)\) và \((2)\) suy ra: Tứ giác \(AMCN\) là hình bình hành ( theo định nghĩa) HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
