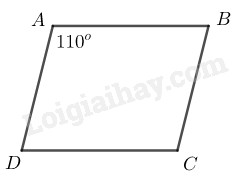
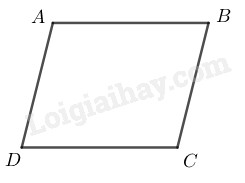
Bài 79 trang 89 SBT toán 8 tập 1Giải bài 79 trang 89 sách bài tập toán 8. Tính các góc của hình bình hành ABCD, biết:... Đề bài Tính các góc của hình bình hành \(ABCD,\) biết: \(a)\) \(\widehat A = {110^0}\) \(b)\) \(\widehat A - \widehat B = {20^0}\) Phương pháp giải - Xem chi tiết Sử dụng kiến thức: +) Trong hình bình hành, hai góc đối bằng nhau. +) Trong hình bình hành, hai góc kề một cạnh bù nhau. Lời giải chi tiết
\(a)\) Tứ giác \(ABCD\) là hình bình hành \( \Rightarrow \widehat C = \widehat A = {110^0}\) (tính chất hình bình hành) Ta có: \(AD//BC\) (do ABCD là hình bình hành) Nên \(\widehat A + \widehat B = {180^0}\) (hai góc trong cùng phía bù nhau) \( \Rightarrow \widehat B = {180^0} - \widehat A = {180^0} - {110^0} = {70^0}\) \(\widehat D = \widehat B = {70^0}\) (tính chất hình bình hành) \(b)\)
Tứ giác \(ABCD\) là hình bình hành nên \(AD//BC\) \( \Rightarrow \widehat A + \widehat B = {180^0}\) (\(2\) góc trong cùng phía bù nhau) \(\widehat A - \widehat B = {20^0}\) \((gt)\) Suy ra: \(\widehat A + \widehat B+\widehat A - \widehat B=180^0+20^0\) \(\Rightarrow 2\widehat A = {200^0} \Rightarrow \widehat A = {100^0}\) \(\widehat C = \widehat A = {100^0}\) ( tính chất hình bình hành) \(\widehat B = \widehat A - {20^0} = {100^0} - {20^0} = {80^0}\) \(\widehat D = \widehat B = {80^0}\) (tính chất hình bình hành) HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
