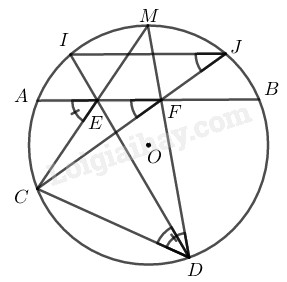
Bài 7.2 phần bài tập bổ sung trang 107 SBT toán 9 tập 2

Đề bài

Cho đường tròn tâm \(O\) bán kính \(R\) và hai dây \(AB,\) \(CD\) bất kì. Gọi \(M\) là điểm chính giữa của cung nhỏ \(AB.\) Gọi \(E\) và \(F\) tương ứng là giao điểm của \(MC,\) \(MD\) với dây \(AB.\) Gọi \(I\) và \(J\) tương ứng là giao điểm của \(DE,\) \(CF\) với đường tròn \((O).\) Chứng minh \(IJ\) song song với \(AB.\)

Lời giải chi tiết

Xét đường tròn \((O)\) có \(M\) là điểm chính giữa của cung nhỏ \(\overparen{AB}\).

Suy ra \(\overparen{MA}\) = \(\overparen{MB}\)

Lại có: \(\widehat {AEC} = \displaystyle {1 \over 2} (sđ\overparen{AC} +sđ \overparen{MB}\)) (góc có đỉnh ở trong đường tròn)

\(\widehat {CDM} = \displaystyle {1 \over 2} sđ\overparen{MAC}\) (tính chất góc nội tiếp) hay \(\widehat {CDF} = \displaystyle  {1 \over 2} (sđ\overparen{MA} + sđ\overparen{AC})\)\(=\displaystyle {1 \over 2} (sđ\overparen{AC} +sđ \overparen{MB})\)

Suy ra: \(\widehat {AEC} = \widehat {CDF}\)

Ta có: \(\widehat {AEC} + \widehat {{\rm{CEF}}} = 180^\circ \) (hai góc kề bù)

Suy ra: \(\widehat {CDF} + \widehat {{\rm{CEF}}} = 180^\circ \) nên tứ giác \(CDFE\) nội tiếp

\( \Rightarrow \widehat {CDE} = \widehat {CFE}\) (\(2\) góc nội tiếp cùng chắn cung nhỏ \(\overparen{CE}\)) hay \(\widehat {CDI} = \widehat {CFE}\)

Trong đường tròn \((O)\) ta có:

\(\widehat {CDI} = \widehat {CJI}\) (\(2\) góc nội tiếp cùng chắn cung nhỏ \(\overparen{CAI}\))

Suy ra: \(\widehat {CJI} = \widehat {CFE}\)

\( \Rightarrow IJ // AB\) (vì có cặp góc ở vị trí đồng vị bằng nhau)

HocTot.Nam.Name.Vn