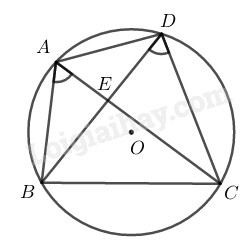
Bài 43 trang 107 SBT toán 9 tập 2Giải bài 43 trang 107 sách bài tập toán 9. Cho hai đoạn thẳng AC và BD cắt nhau tại E... Đề bài Cho hai đoạn thẳng \(AC\) và \(BD\) cắt nhau tại \(E.\) Biết \(AE.EC = BE.ED\). Chứng minh bốn điểm \(A, B, C, D \)cùng nằm trên một đường tròn. Phương pháp giải - Xem chi tiết Ta sử dụng kiến thức: +) Các điểm cùng nhìn một cạnh cố định dưới góc bằng nhau thì các điểm đó cùng thuộc một cung chứa góc vẽ trên cạnh cố định. +) Một tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn. Lời giải chi tiết
Từ \(AE. EC =BE. ED \;\;(gt)\) \( \Rightarrow \displaystyle {{AE} \over {ED}} = {{BE} \over {EC}}\) Xét \(∆AEB\) và \(∆DEC:\) \(\displaystyle {{AE} \over {ED}} = {{BE} \over {EC}}\) \(\widehat {AEB} = \widehat {DEC}\) (đối đỉnh) Suy ra: \(∆AEB\) đồng dạng \(∆DEC\;\; (c.g.c)\) \( \Rightarrow \widehat {BAE} = \widehat {CDE}\) hay \(\widehat {BAC} = \widehat {CDB}\) Từ đó: \(A\) và \(D\) nhìn đoạn \(BC\) cố định dưới một góc bằng nhau nên \(4\) điểm \(A,B, C, D\) nằm trên một đường tròn. HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
