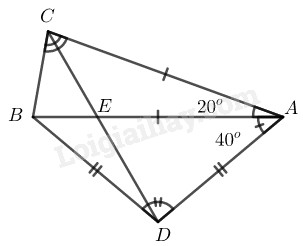
Bài 41 trang 106 SBT toán 9 tập 2

Đề bài

Cho tam giác cân \(ABC\) có đáy \(BC\) và \(\widehat A = {20^0}\). Trên nửa mặt phẳng bờ \(AB\) không chứa điểm \(C\) lấy điểm \(D\) sao cho \(DA = DB\) và \(\widehat {DAB} = {40^0}\). Gọi \(E\) là giao điểm của \(AB\) và \(CD.\)

\(a)\) Chứng minh \(ACBD\) là tứ giác nội tiếp

\(b)\) Tính \(\widehat {AED}\)

Lời giải chi tiết

\(a)\) \(∆ABC\) cân tại \(A \;\;(gt).\)

\( \Rightarrow \widehat {ACB} = \widehat {ABC}\) (tính chất tam giác cân)

\( \Rightarrow \widehat {ACB} =\displaystyle {{180^\circ  - \widehat A} \over 2} \)\(= \displaystyle {{180^\circ  - 20^\circ } \over 2} = 80^\circ \)

\(∆DAB\) cân tại \(D\) (do \(DA=DB)\)

\( \Rightarrow \widehat {DBA} = \widehat {DAB}\) (tính chất tam giác cân) mà \(\widehat {DAB} = 40^\circ \) (gt) \( \Rightarrow \widehat {DBA} = 40^\circ \)

\(\widehat {ADB} = 180^\circ  - (\widehat {DAB} + \widehat {DBA})\)\( = 180^\circ  - (40^\circ  + 40^\circ ) = 100^\circ \)

Trong tứ giác \(ACBD\) ta có: \(\widehat {ACB} + \widehat {ADB} \)\(= 80^\circ  + 100^\circ  = 180^\circ \)

Vậy: Tứ giác \(ACBD\) nội tiếp.

\(b)\) Vì tứ giác \(ACBD\) nội tiếp (câu a) nên xét đường tròn ngoại tiếp tứ giác \(ACBD\) ta có:

+) \(\widehat {BAC} =\displaystyle  {1 \over 2} sđ \overparen{BC}\) (tính chất góc nội tiếp)

\( \Rightarrow \) sđ \(\overparen{BC}\)\( = 2\widehat {BAC} = 2.20^\circ  = 40^\circ \)

+) \(\widehat {DBA} =\displaystyle {1 \over 2}sđ \overparen{AD}\) (tính chất góc nội tiếp)

\( \Rightarrow \) sđ \(\overparen{AD}\) \( = 2\widehat {DBA} = 2.40^\circ  = 80^\circ \)

+) \(\widehat {AED}\) là góc có đỉnh ở trong đường tròn ngoại tiếp tứ giác \(ACBD\)

\(\widehat {AED} =\displaystyle  {1 \over 2}(sđ \overparen{BC} + sđ \overparen{AD})\) \( = \displaystyle {{40^\circ  + 80^\circ } \over 2} = 60^\circ \)

HocTot.Nam.Name.Vn