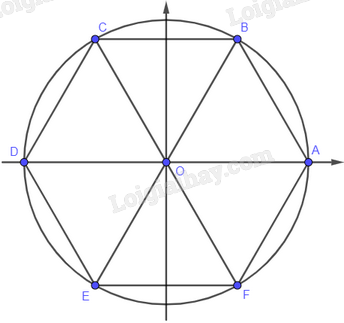
Giải bài 63 trang 31 sách bài tập toán 11 - Cánh diều

Đề bài

Cho lục giác đều $ABCDEF$ nội tiếp trong đường tròn lượng giác (thứ tự đi từ $A$ đến các đỉnh theo chiều dương). Khi đó, số đo của góc lượng giác $\left( {OA,OC} \right)$ bằng:

A. $\frac{{2\pi }}{3} + k2\pi$                                              

B. $- \frac{{2\pi }}{3} + k2\pi$

C. $\frac{\pi }{3} + k2\pi$                                         

D. $- \frac{\pi }{3} + k2\pi$

Lời giải chi tiết

Vì lục giác đều $ABCDEF$ nội tiếp đường tròn lượng giác tâm $O$, nên ta có 6 góc bằng nhau: $\widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOF} = \widehat {FOA} = {60^o} = \frac{\pi }{3}$

Do đó $\widehat {AOC} = \frac{{2\pi }}{3} \Rightarrow \left( {OA,OC} \right) = \frac{{2\pi }}{3} + k2\pi$

Đáp án đúng là A.