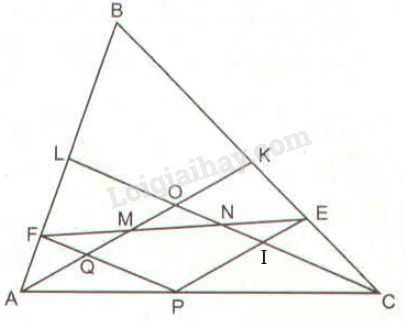
Bài 60 trang 98 SBT toán 8 tập 2

Đề bài

Tam giác $ABC$ có hai trung tuyến $AK$ và $CL$ cắt nhau tại $O.$ Từ một điểm $P$ bất kì trên cạnh $AC$, vẽ các đường thẳng $PE$ song song với $AK,$ $PF$ song song với $CL$ ($E$ thuộc $BC,$ $F$ thuộc $AB$). Các trung tuyến $AK, CL$ cắt đoạn thẳng $EF$ theo thứ tự tại $M, N$.

Chứng minh rằng các đoạn thẳng $FM, MN, NE$ bằng nhau. 

Lời giải chi tiết

Gọi $Q$ là giao điểm của $PF$ và $AK,$ $I$ là giao điểm của $PE$ và $CL.$

Vì $O$ là giao của hai đường trung tuyến $AK, CL$ nên $O$ là trọng tâm tam giác $ABC$

Suy ra $\displaystyle LO = {1 \over 3} CL$ và $OK = \displaystyle{1 \over 3}AK$ (tính chất trọng tâm)

Trong tam giác $FPE$ có $PE // AK$ hay $QM // PE$

Theo định lí Ta-lét ta có: $\displaystyle {{FQ} \over {FP}} = {{FM} \over {FE}}$  (1)

Trong tam giác $ALO$ có $PF // CL$ hay $FQ // LO$

Theo hệ quả định lí Ta-lét ta có: $\displaystyle  {{AF} \over {AL}} = {{FQ} \over {LO}}$    (2)

Trong tam giác $ALC$ có $PF // CL$

Theo hệ quả định lí Ta-lét ta có: $\displaystyle{{AF} \over {AL}} = {{FP} \over {CL}}$    (3)

Từ (2) và (3) suy ra $\displaystyle{{FQ} \over {LO}} = {{FP} \over {CL}}$$\displaystyle\,\Rightarrow {{FQ} \over {FP}} = {{LO} \over {CL}}$

Vì $\displaystyle LO = {1 \over 3} CL$ (chứng minh trên) nên $\displaystyle{{FQ} \over {FP}} = {1 \over 3}$          (4)

Từ (1) và (4) suy ra $\displaystyle{{FM} \over {FE}} = {1 \over 3}$$\,\displaystyle\Rightarrow FM = {1 \over 3}FE$

Trong tam giác $EPF$ có $PF // CL$ hay $NI // PF$

Theo định lí Ta-lét ta có: $\displaystyle{{EI} \over {EP}} = {{EN} \over {EF}}$    (5)

Trong tam giác $CKO$ có $EI // OK$

Theo hệ quả định lí Ta-lét ta có: $\displaystyle{{CE} \over {CK}} = {{EI} \over {KO}}$  (6)

Trong tam giác $CKA$ có $PE // AK$

Theo hệ quả định lí Ta-lét ta có: $\displaystyle {{CE} \over {CK}} = {{EP} \over {AK}}$   (7)

Từ (6) và (7) suy ra: $\displaystyle {{EI} \over {OK}} = {{EP} \over {AK}}$ $\displaystyle  \Rightarrow {{EI} \over {EP}} = {{OK} \over {AK}}$

Vì $OK = \displaystyle{1 \over 3}AK$ (chứng minh trên) nên $\displaystyle{{EI} \over {EP}} = {1 \over 3}$                   (8)

Từ (5) và (8) suy ra: $\displaystyle {{EN} \over {EF}} = {1 \over 3}$$\,\displaystyle \Rightarrow EN = {1 \over 3}EF$

Ta có:

$\eqalign{  & MN = EF - \left( {EN + FM} \right)  \cr  & \;\;\;\;\;\; \;\;= EF - \left( {{1 \over 3}EF + {1 \over 3}EF} \right) \cr&\;\;\;\;\;\;\;\;= {1 \over 3}EF \cr}$

Vậy $EN = MN = MF.$

HocTot.Nam.Name.Vn