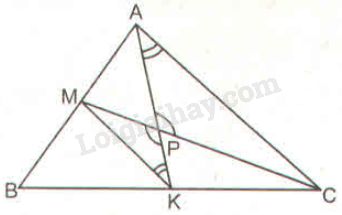
Bài 56 trang 98 SBT toán 8 tập 2

Đề bài

Hai điểm \(M\) và \(K\) thứ tự nằm trên cạnh \(AB\) và \(BC\) của tam giác \(ABC\); hai đoạn thẳng \(AK\) và \(CM\) cắt nhau tại điểm \(P.\) Biết rằng \(AP = 2 PK\) và \(CP = 2PM.\)

Chứng minh rằng \(AK\) và \(CM\) là các trung tuyến của tam giác \(ABC.\)

Lời giải chi tiết

\(AP = 2 PK\) và \(CP = 2PM\) (gt)

\( \Rightarrow \displaystyle{{PK} \over {PA}} = {1 \over 2};{{PM} \over {PC}} = {1 \over 2}\)

\( \Rightarrow\displaystyle {{PK} \over {PA}} = {{PM} \over {PC}} = {1 \over 2}\)

Xét \(∆ PKM\) và \(∆ PAC\) có:

\(\displaystyle {{PK} \over {PA}} = {{PM} \over {PC}}\) (chứng minh trên)

\(\widehat {APC} = \widehat {KPM}\) (đối đỉnh)

\( \Rightarrow ∆ PKM\) đồng dạng \(∆ PAC\) (c.g.c) với tỉ số đồng dạng \(k =\displaystyle {{PK} \over {PA}}= {1 \over 2}\).

\( \Rightarrow\displaystyle {{KM} \over {AC}} = {1 \over 2}\)                          (1)

Vì \(∆ PKM\) đồng dạng \(∆ PAC\) suy ra \(\widehat {PKM} = \widehat {PAC}\)

Mà \(\widehat {PKM} \) và \( \widehat {PAC}\) ở vị trí so le trong nên \( KM // AC\) (vì có cặp góc ở vị trí so le trong bằng nhau).

Trong tam giác \(ABC\) có \(KM // AC\) nên \(\widehat {BMK} = \widehat {BAC}\) (hai góc đồng vị)

Lại có góc \(B\) chung nên \( ∆ BMK\) đồng dạng \(∆ BAC\) (g.g)

\( \Rightarrow\displaystyle  {{BM} \over {BA}} = {{BK} \over {BC}} = {{MK} \over {AC}}\)     (2)

Từ (1) và (2) suy ra: \(\displaystyle {{BM} \over {BA}} = {{BK} \over {BC}} = {1 \over 2}\)

Do đó \(BM = \displaystyle {1 \over 2} BA\) nên \(M\) là trung điểm của \(AB\).

\(BK =\displaystyle  {1 \over 2} BC\) nên \(K\) là trung điểm của \(BC\).

Vậy \(AK\) và \(CM\) là đường trung tuyến của tam giác \(ABC.\)

HocTot.Nam.Name.Vn