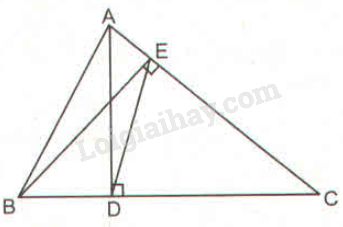
Bài 59 trang 98 SBT toán 8 tập 2Giải bài 59 trang 98 sách bài tập toán 8. Tam giác ABC có hai đường cao là AD và BE (D thuộc BC, E thuộc AC)... Đề bài Tam giác \(ABC\) có hai đường cao là \(AD\) và \(BE\) (\(D\) thuộc \(BC,\) \(E\) thuộc \(AC\)). Chứng minh hai tam giác \(DEC\) và \(ABC\) là hai tam giác đồng dạng. Phương pháp giải - Xem chi tiết Sử dụng: - Nếu hai cạnh tam giác này tỉ lệ với hai cạnh của tam giác kia và góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đồng dạng. - Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng. Lời giải chi tiết
Xét \(∆ ADC\) và \(∆ BEC\) có: +) \(\widehat {ADC} = \widehat {BEC} = 90^\circ \) +) \(\widehat C\) chung \( \Rightarrow ∆ ADC \backsim ∆ BEC\) (g.g) \( \Rightarrow\displaystyle{{AC} \over {BC}} = {{DC} \over {EC}}\)(2 cặp cạnh tương ứng tỉ lệ) \( \Rightarrow\displaystyle {{EC} \over {BC}} = {{DC} \over {AC}}\) Xét \(∆ DEC\) và \(∆ ABC\) có: +) \(\displaystyle {{EC} \over {BC}} = {{DC} \over {AC}}\) (chứng minh trên) +) \(\widehat C\) chung \( \Rightarrow ∆ DEC\backsim ∆ ABC\) (c.g.c) HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
