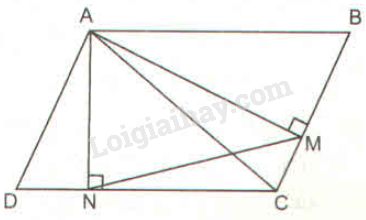
Bài 57 trang 98 SBT toán 8 tập 2Giải bài 57 trang 98 sách bài tập toán 8. Cho hình bình hành ABCD. Từ A kẻ AM vuông góc với BC, AN vuông góc với CD (M thuộc BC và N thuộc CD). Đề bài Cho hình bình hành \(ABCD.\) Từ \(A\) kẻ \(AM\) vuông góc với \(BC,\) \(AN\) vuông góc với \(CD\) (\(M\) thuộc \(BC\) và \(N\) thuộc \(CD\)). Chứng minh rằng tam giác \(MAN\) đồng dạng với tam giác \(ABC.\) Phương pháp giải - Xem chi tiết Sử dụng: - Nếu hai cạnh tam giác này tỉ lệ với hai cạnh của tam giác kia và góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đồng dạng. - Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng. Lời giải chi tiết * Trường hợp \(\widehat B\) nhọn:
Xét \(∆ AMB\) và \(∆ AND\) có: \(\widehat {AMB} = \widehat {AND} = 90^\circ \) \(\widehat B = \widehat D\) (vì \(ABCD\) là hình bình hành) \( \Rightarrow ∆ AMB\) đồng dạng \(∆ AND\) (g.g) \( \displaystyle \Rightarrow {{AM} \over {AB}} = {{AN} \over {AD}} \) Mà \(AD = BC\) (vì \(ABCD\) là hình bình hành) \( \displaystyle \Rightarrow {{AM} \over {AB}} = {{AN} \over {BC}}\) Lại có: \(AB // CD\) (gt) \(AN ⊥ CD\) (gt) \(\Rightarrow AN ⊥ AB\) hay \(\widehat {NAB} = {90^o}\). \(\Rightarrow \widehat {NAM} + \widehat {MAB} = 90^\circ \) (1) Trong tam giác vuông \(AMB\) có \(\widehat {AMB} = 90^\circ \) \(\Rightarrow \widehat {MAB} + \widehat B = 90^\circ \) (2) Từ (1) và (2) suy ra: \(\widehat {NAM} = \widehat B\) Xét \(∆ ABC\) và \(∆ MAN\) có: \( \displaystyle{{AM} \over {AB}} = {{AN} \over {BC}}\) (chứng minh trên) \(\widehat {NAM} = \widehat B\) (chứng minh trên) \(\Rightarrow ∆ ABC\) đồng dạng \(∆ MAN \) (c.g.c) * Trường hợp \(\widehat B\) tù:
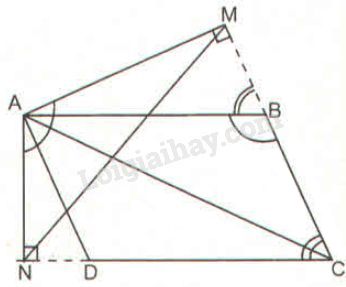
\(ABCD\) là hình bình hành nên \(AB//CD;\;AD//BC\). Vì \(AB//CD\) nên \(\widehat {ABM} =\widehat C\) (cặp góc đồng vị). Vì \(AD//BC\) nên \(\widehat {ADN}=\widehat C\) (cặp góc đồng vị). Xét \(∆ AMB\) và \(∆ AND\) có: \(\widehat {AMB} = \widehat {AND} = 90^\circ \) \(\widehat {ABM} = \widehat {ADN}\) (vì cùng bằng \(\widehat C\)) \(\Rightarrow ∆ AMB\) đồng dạng \(∆ AND\) (g.g) \( \displaystyle \Rightarrow {{AM} \over {AB}} = {{AN} \over {AD}}\) Mà \(AD = BC\) (vì \(ABCD\) là hình bình hành) \( \displaystyle \Rightarrow{{AM} \over {AB}} = {{AN} \over {BC}}\) Vì \(AB // CD\) nên \(\widehat {ABC} + \widehat C = 180^\circ \) (cặp góc trong cùng phía) (3) Tứ giác \(AMCN\) có \(\widehat {AMC} = \widehat {AND} = 90^\circ \) \(\Rightarrow \widehat {MAN} + \widehat C = 180^\circ \) (4) Từ (3) và (4) suy ra \(\widehat {MAN} = \widehat {ABC}\) Xét \(∆ MAN\) và \(∆ ABC\) có: \( \displaystyle {{AM} \over {AB}} = {{AN} \over {BC}}\) (chứng minh trên) \(\widehat {MAN} = \widehat {ABC}\) (chứng minh trên) \(\Rightarrow ∆ MAN\) đồng dạng \(∆ ABC\) (c.g.c) HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
