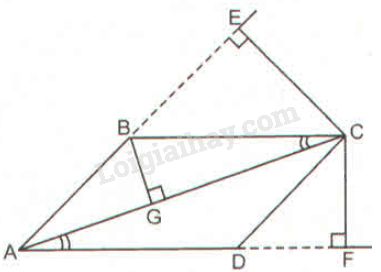
Bài 58 trang 98 SBT toán 8 tập 2

Đề bài

Giả sử \(AC\) là đường chéo lớn của hình bình hành \(ABCD.\) Từ \(C\), vẽ đường vuông góc \(CE\) với đường thẳng \(AB\), đường vuông góc \(CF\) với đường thẳng \(AD\) (\(E,F \) thuộc phần kéo dài của các cạnh \(AB\) và \(AD\)). Chứng minh rằng: \(AB.AE + AD.AF = A{C^2}\). 

Lời giải chi tiết

Dựng \(BG ⊥ AC.\)

Xét \(∆ BGA\) và \(∆ CEA\) có:

+) \(\widehat {BGA} = \widehat {CEA} = 90^\circ \)

+) \(\widehat A\) chung

\( \Rightarrow  ∆ BGA\) đồng dạng \(∆ CEA \) (g.g)

\( \displaystyle\Rightarrow {{AB} \over {AC}} = {{AG} \over {AE}}\)

\(\Rightarrow AB.AE = AC.AG\)      (1)

Vì \(AD//BC\) nên \(\widehat {BCG} = \widehat {CAF}\)  (cặp góc so le trong)

Xét \(∆ BGC\) và \(∆ CFA\) có:

+) \(\widehat {BGC} = \widehat {CFA} = 90^\circ \)

+) \(\widehat {BCG} = \widehat {CAF}\) (cmt)

\(\Rightarrow ∆ BGC\) đồng dạng \(∆ CFA\) (g.g)

\( \displaystyle\Rightarrow {{AF} \over {CG}} = {{AC} \over {BC}}\)

\(\Rightarrow BC.AF = AC.CG\)

Mà \(BC = AD\) (vì \(ABCD\) là hình bình hành)

\(\Rightarrow AD.AF = AC.CG \)           (2)

Cộng từng vế của đẳng thức (1) và (2) ta có:

\(AB.AE + AD.AF\)\(\, = AC.AG + AC.CG\)

\( \Rightarrow AB.AE + AD.AF \)\(\,= AC\left( {AG + CG} \right)\)

Lại có: \(AG + CG = AC\) nên \(AB.AE + AD.AF = A{C^2}\).

HocTot.Nam.Name.Vn