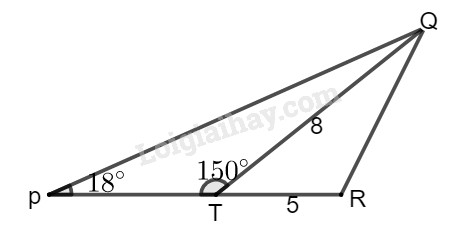
Bài 60 trang 115 SBT toán 9 tập 1

Đề bài

Cho hình:

  

Biết:

\(\widehat {QPT} = 18^\circ \),

\(\widehat {PTQ} = 150^\circ \),

     \(QT = 8cm,\)

     \(TR = 5cm.\)

Hãy tính:

a)   \(PT;\)

b)   Diện tích tam giác \(PQR.\) 

Lời giải chi tiết

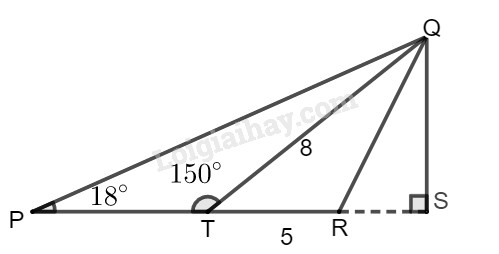
a) Kẻ \(QS \bot PR\)

Ta có: \(\widehat {QTS} = 180^\circ  - \widehat {QTP}\)\( = 180^\circ  - 150^\circ  = 30^\circ \)

Trong tam giác vuông \(QST\), ta có:   

\(QS = QT.\sin \widehat {QTS} \)\(= 8.\sin 30^\circ  = 4\left( {cm} \right)\)

\(TS = QT.c{\rm{os}}\widehat {QTS} \)\(= 8.c{\rm{os30}}^\circ  \approx 6,928\left( {cm} \right)\)

Trong tam giác vuông \(QSP\), ta có:

\(SP = QS.\cot g\widehat {QPS}\)\( = 4.\cot g18^\circ   \approx 12,311\left( {cm} \right)\)

\(PT = SP - TS \approx 12,311 - 6,928\)\( = 5,383\left( {cm} \right)\)

b) Ta có:  

\(\displaystyle {S_{\Delta QPR}} = {1 \over 2}.QS.PR\)\( = \dfrac{1}{2}.QS.(PT + TR)\)

\( \approx \dfrac{1}{2}.4.(5,383 + 5) \)\(= 2.10,383 = 20,766\left( {c{m^2}} \right)\)

HocTot.Nam.Name.Vn