Bài 61 trang 115 SBT toán 9 tập 1Giải bài 61 trang 115 sách bài tập toán 9. Cho BCD là tam giác đều cạnh 5cm và góc DBA bằng 40°. Đề bài Cho \(BCD\) là tam giác đều cạnh \(5cm\) và góc \(DBA\) bằng \(70^\circ \).
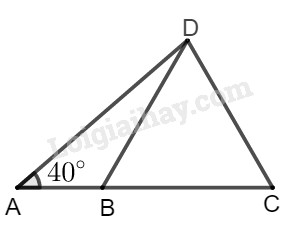
Hãy tính: a) \(AD;\) b) \(AB.\) Phương pháp giải - Xem chi tiết Cho hình vẽ:
Ta có: \(\sin \alpha = \dfrac{{AB}}{{BC}}\) nên \(AB=BC.\sin \alpha , \) \(BC = \dfrac{{AB}}{{\sin \alpha }}\) và \(\cot \alpha = \dfrac{{AC}}{{AB}}.\) Lời giải chi tiết
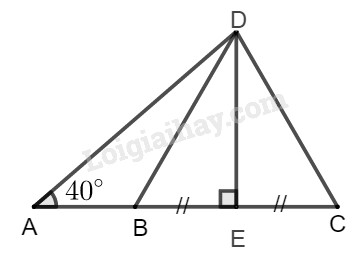
a) Kẻ \(DE \bot BC\) Suy ra: \(BE = EC = \dfrac{1}{2}BC = 2,5\left( {cm} \right)\) Trong tam giác vuông \(BDE\), ta có: \(DE = BD.\sin \widehat {DBE}\)\( = 5.\sin 60^\circ = \dfrac{{5\sqrt 3 }}{2}\left( {cm} \right)\) Trong tam giác vuông \(ADE\), ta có: \(AD = \dfrac{{DE}}{{\sin \widehat A}} = \dfrac{{\dfrac{{5\sqrt 3 }}{2}}}{{\sin 40^\circ }}\)\( \approx 6,736\left( {cm} \right)\) b) Trong tam giác vuông \(ADE\), ta có: \(AE = AD.\cot g\ A \)\(\approx 6,736.\cot 40^\circ = 5,16\left( {cm} \right)\) Ta có: \(AB = AE - BE\)\( = 5,16 - 2,5 = 2,66\left( {cm} \right)\) HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
