Bài 64 trang 115 SBT toán 9 Tập 1Giải bài 64 trang 115 sách bài tập toán 9. Tính diện tích của hình bình hành có hai cạnh 12cm và 15cm, góc tạo bởi hai cạnh ấy bằng 100 độ. Đề bài Tính diên tích của hình bình hành có hai cạnh \(12\,cm\) và \(15\,cm,\) góc tạo bởi hai cạnh ấy bằng \(100\)\(^\circ \). Phương pháp giải - Xem chi tiết Áp dụng các hệ thức về cạnh và góc trong tam giác vuông, tam giác \(ABC\) vuông tại \(A\) có \(AB=c,\,AC=b,\, BC=a\) thì: \(b=a.sin\,B=a.cos\,C\) Diện tích hình bình hành bằng tích chiều cao với cạnh đáy tương ứng. Lời giải chi tiết
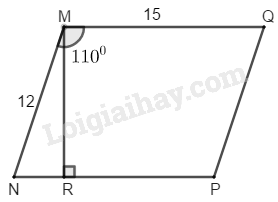
Giả sử hình bình hành \(MNPQ\) có \(MN = 12\,cm,\, MQ = 15\,cm,\) \(\widehat {NMQ} = 110^\circ \) Ta có: \(\widehat {NMQ} + \widehat {MNP} = 180^\circ \) (hai góc trong cùng phía) Suy ra: \(\widehat {MNP} = 180^\circ - \widehat {NMQ}\) \( = 180^\circ - 110^\circ = 70^\circ \) Kẻ \(MR \,\bot\, NP\) Trong tam giác vuông \(MNR,\) ta có: \(\eqalign{ Vậy \({S_{MNPQ}} = MR.MQ \approx 11,276.15\) \(= 169,14\) \((cm^2).\) HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
