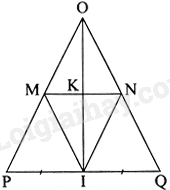
Giải bài 6 trang 45 sách bài tập toán 8 - Chân trời sáng tạo tập 2

Đề bài

Cho tam giác OPQ cân tại O có I là trung điểm của PQ. Kẻ IM//QO$\left( {M \in OP} \right)$, IN//PO $\left( {N \in QO} \right)$. Chứng minh:

a) Tam giác IMN cân tại I.

b) OI là đường trung trực của MN.

Lời giải chi tiết

a) Tam giác OPQ có: $IP = IQ$, IM//QO nên $MO = MP$

Tam giác OPQ có: $IP = IQ$, $MO = MP$ nên IM là đường trung bình của tam giác OPQ, suy ra $IM = \frac{1}{2}QO$

Tương tự ta có: $IN = \frac{1}{2}PO$.

Mà $PO = QO$ (do tam giác POQ cân tại O) nên $IM = IN$, suy ra tam giác IMN cân tại I.

b) Gọi K là giao điểm của IO và MN.

Tam giác OPQ có: $MO = MP$, $NO = NQ$ nên MN là đường trung bình của tam giác OPQ, suy ra MN//PQ (1).

Tam giác OPQ cân tại O có OI là đường trung tuyến nên OI cũng là đường cao của tam giác OPQ.

Suy ra: $OI \bot PQ$ (2)

Từ (1) và (2) suy ra: $MN \bot OI$ tại K hay $MN \bot IK$

Mà tam giác IMN cân tại I nên IK là đường trung trực của MN hay OI là đường trung trực của MN.