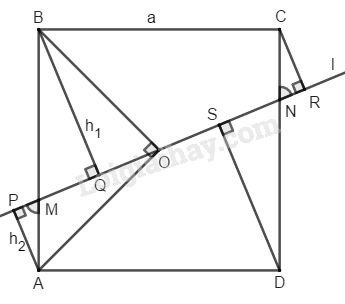
Bài 53 trang 166 SBT toán 8 tập 1

Đề bài

Qua tâm $O$ của hình vuông $ABCD$ cạnh $a,$ kẻ đường thẳng $l$ cắt cạnh $AB$ và $CD$ lần lượt tại $M$ và $N.$ Biết $MN = b.$ Hãy tính tổng các khoảng cách từ các đỉnh của hình vuông đến đường thẳng $l$ theo $a$ và $b$ ($a$ và $b$ có cùng đơn vị đo)

Lời giải chi tiết

Gọi $h_1$ và $h_2$  là khoảng cách từ đỉnh $B$ và đỉnh $A$ đến đường thẳng $l$; gọi tổng khoảng cách là $S.$

Vì $O$ là tâm đối xứng của hình vuông.

$⇒ OM = ON,OA=OC$ (tính chất đối xứng tâm)

Suy ra: $AM = CN$ (đối xứng qua $O$)

$\widehat {AMP} = \widehat {DNS}$ (đồng vị)

$\widehat {DNS} = \widehat {CNR}$ (đối đỉnh)

$\Rightarrow \widehat {AMP} = \widehat {CNR}$

Suy ra: $∆ APM = ∆ CRN$ (cạnh huyền, góc nhọn)

$⇒ CR = AP =h_2$ 

$AM = CN$ (hai cạnh tương ứng)

$⇒ BM = DN$

$\widehat {BMQ} = \widehat {DNS}$ (so le trong)

Suy ra: $∆ BQM = ∆ DSN$ (cạnh huyền, góc nhọn) $⇒ DS = BQ =h_1$

$\eqalign{  & {S_{BOA}} = {1 \over 4}{S_{ABCD}} = {1 \over 4}{a^2}\,(1) }$ 

$\eqalign{{S_{BOA}} = {S_{BOM}} + {S_{AOM}} }$

$\eqalign{= {1 \over 2}{b \over 2}.{h_1} + {1 \over 2}{b \over 2}.{h_2} }$ 

$\eqalign{= {b \over 4}\left( {{h_1} + {h_2}} \right)\,(2) }$

Từ $(1)$ và $(2):$ ${h_1} + {h_2} = \dfrac{{{a^2}}}{b}$

$S = 2\left( {{h_1} + {h_2}} \right) = \dfrac{{2{a^2}} }{ b}$

HocTot.Nam.Name.Vn