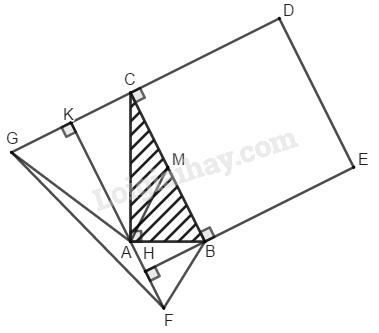
Bài 56 trang 166 SBT toán 8 tập 1

Đề bài

Cho tam giác \(ABC\) vuông ở \(A\) và có \(BC = 2 AB = 2a.\) Ở phía ngoài tam giác, ta vẽ hình vuông \(BCDE,\) tam giác đều \(ABF\) và tam giác đều \(ACG.\)
a) Tính các góc \(B,\, C,\) cạnh \(AC\) và diện tích tam giác \(ABC.\)
b) Chứng minh rằng \(FA\) vuông góc với \(BE\) và \(CG.\) Tính diện tích các tam giác \(FAG\) và \(FBE.\)
c) Tính diện tích tứ giác \(DEFG.\)

Lời giải chi tiết

a) Gọi \(M\) là trung điểm của \(BC,\) ta có:

\(AM = MB =\) \(\eqalign{1 \over 2}BC = a\) (tính chất tam giác vuông) \(⇒ AM = MB = AB = a\)

nên \(∆ AMB\) đều ⇒ \(\widehat {ABC} = 60^\circ \)

Mặt khác : \(\widehat {ABC} + \widehat {ACB} = 90^\circ \) (tính chất tam giác cân)

Suy ra: \(\widehat {ACB} = 90^\circ  - \widehat {ABC}\) \(= 90^\circ  - 60^\circ  = 30^\circ \)

Trong tam giác vuông \(ABC,\) theo định lý Pi-ta-go ta có :

\(B{C^2} = A{B^2} + A{C^2}\)

Suy ra: \(\eqalign{ A{C^2} = B{C^2} - A{B^2} }\) \(= 4{a^2} - {a^2} = 3{a^2} \)

Hay \(AC = a\sqrt 3  \)

Do đó ta có diện tích \(∆ ABC\) là: \(S_{ABC}=\dfrac{1}{2}AB.AC\) \(=\dfrac{1}{2}.a.a\sqrt 3=\dfrac{1}{2}a^2\sqrt 3\)

b)  Ta có : \(\widehat {FAB} = \widehat {ABC} = 60^\circ \)

\(⇒ FA // BC\) (vì có cặp góc ở vị trí so le trong bằng nhau)

Suy ra: \(FA ⊥ BE\)

\(BC ⊥ CD\) (vì \(BCDE\) là hình vuông)

Suy ra: \(FA ⊥ CD\)

Gọi giao điểm \(BE\) và \(FA\) là \(H, FA\) và \(CG\) là \(K.\)

\( \Rightarrow BH \bot FA\) và \(FH = HA =\) \(\eqalign{a \over 2}\) (tính chất tam giác đều)

\(\widehat {ACG} + \widehat {ACB} + \widehat {BCD} \) \(= 60^\circ  + 30^\circ  + 90^\circ  = 180^\circ \)

\(⇒ G, C, D\) thẳng hàng

\(⇒ AK ⊥ CG\) và \(GK = KC\) \(= \eqalign{1 \over 2} GC \) = \(\eqalign{1 \over 2}AC \) \(= \eqalign{{a\sqrt 3 } \over 2}\)

\({S_{FAG}} = \eqalign{1 \over 2}GK.AF =\eqalign {1 \over 2}.\eqalign{{a\sqrt 3 } \over 2}.a \) \(=\eqalign {{{a^2}\sqrt 3 } \over 4}\)  (đvdt)

\({S_{FBE}} = \eqalign{1 \over 2}FH.BE =\eqalign {1 \over 2}.\eqalign{a \over 2}.2a \) \(= \eqalign{1 \over 2}{a^2}\) (đvdt)

c) \({S_{BCDE}} = B{C^2} = {\left( {2a} \right)^2} = 4{a^2}\) (đvdt)

Trong tam giác vuông \(BHA,\) theo định lý Pi-ta-go ta có:

\(\eqalign{  & A{H^2} + B{H^2} = A{B^2} }\) \(  \Rightarrow B{H^2} = A{B^2} - A{H^2}\) \(= {a^2} - \eqalign{{{a^2}} \over 4} = \eqalign{{3{a^2}} \over 4} \) \(\Rightarrow BH = \eqalign{{a\sqrt 3 } \over 2}  \)

\(\displaystyle {S_{ABF}} = {1 \over 2}BH.FA = \eqalign{1 \over 2}.\eqalign{{a\sqrt 3 } \over 2}.a \) \(= \eqalign{{{a^2}\sqrt 3 } \over 4}\)  (đvdt)

Trong tam giác vuông \(AKC,\) theo định lý Pi-ta-go ta có:

\(A{C^2} = A{K^2} + K{C^2}\)

\(\eqalign{ \Rightarrow A{K^2} = A{C^2} - K{C^2}}\) \( {= 3{a^2} - \eqalign{{3{a^2}} \over 4} = \eqalign{{9{a^2}} \over 4}}\) \(\Rightarrow {AK = \eqalign{{3a} \over 2} } \)

\({S_{ACG}} = \eqalign{1 \over 2}AK.CG = \eqalign{1 \over 2}.\eqalign{{3a} \over 2}.a\sqrt 3 \) \(= \eqalign{{3{a^2}\sqrt 3 } \over 4}\)  (đvdt)

\({S_{DEFG}} = {S_{BCDE}} + {S_{FBE}} + {S_{FAB}} \) \(+ {S_{FAG}} + {S_{ACG}}+ {S_{ACB}}\)

\( = 4{a^2} + \eqalign{{{a^2}} \over 2} + \eqalign{{{a^2}\sqrt 3 } \over 4} + \eqalign{{{a^2}\sqrt 3 } \over 4} \) \(+ \eqalign{{3{a^2}\sqrt 3 } \over 4} +\dfrac{1}{2}a^2\sqrt 3= \eqalign{{{a^2}} \over 4}\left( {18 + 7\sqrt 3 } \right)\) (đvdt) 

HocTot.Nam.Name.Vn