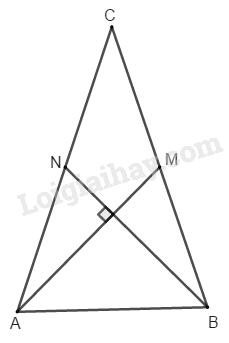
Bài 54 trang 166 SBT toán 8 tập 1

Đề bài

Tam giác $ABC$ có hai trung tuyến $AM$ và $BN$ vuông góc với nhau. Hãy tính diện tích tam giác đó theo $AM$ và $BN$

Lời giải chi tiết

Tứ giác $ABMN$ có hai đường chéo vuông góc.

${S_{ABMN}} = \eqalign{1 \over 2}AM.BN$

$∆ ABM$ và $∆ AMC$ có chung chiều cao kẻ từ $A,$ cạnh đáy $BM = MC$

$\Rightarrow {S_{ABM}} = {S_{AMC}} = \eqalign{1 \over 2}{S_{ABC}}$

$∆ MAN$ và $∆ MNC$ có chung chiều cao kẻ từ $M,$ cạnh đáy $AN = NC$

$\eqalign{  &  \Rightarrow {S_{MAN}} = {S_{MNC}} = {1 \over 2}{S_{AMC}} }$ $\eqalign{ = {1 \over 4} {S_{ABC}}}$  

$\eqalign{{S_{ABMN}} = {S_{ABM}} + {S_{MNA}}}$ 

$= \eqalign{{1 \over 2}{S_{ABC}} + {1 \over 4}{S_{ABC}} }$

$= \eqalign{{3 \over 4}{S_{ABC}} }$ 

$\Rightarrow \eqalign{{S_{ABC}} = \eqalign{4 \over 3}{S_{ABMN}} }$ $= \eqalign{{4 \over 3}.\eqalign{1 \over 2}.AM.BN =\eqalign {2 \over 3}AM.BN }$

HocTot.Nam.Name.Vn