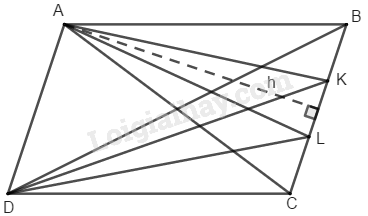
Bài 55 trang 166 SBT toán 8 tập 1

Đề bài

Cho hình bình hành \(ABCD.\) Gọi \(K\) và \(L\) là hai điểm thuộc cạnh \(BC\) sao cho \(BK = KL = LC.\) Tính tỉ số diện tích của :

a) Các tam giác \(DAC\) và \(DCK\)

b) Tam giác \(DAC\) và tứ giác \(ADLB\)

c) Các tứ giác \(ABKD\) và \(ABLD\)

Lời giải chi tiết

a) Ta có: \({S_{ACD}} = {S_{BCD}} = {S_{DAB}} = {S_{CAB}} \) \(=\eqalign {1 \over 2}{S_{ABCD}}\) (1)

\(∆ DCK\) và \(∆ DCB\) có chung chiều cao kẻ từ đỉnh \(D,\) cạnh đáy \(CK = \eqalign{2 \over 3}CB\)

\( \Rightarrow {S_{DCK}} =\eqalign {2 \over 3}{S_{DBC}}\)  (2)

Từ (1) và (2) suy ra: \({S_{DCK}} = \eqalign{2 \over 3}{S_{DAC}} \Rightarrow \eqalign{{{S_{DCK}}} \over {{S_{DAC}}}} = \eqalign{2 \over 3}\)

b) Ta có: \({S_{ADLB}} = {S_{ADB}} + {S_{DLB}}\)

\(∆ DBC\) và \(∆ DLC\) có chung chiều cao kẻ từ đỉnh \(D,\) cạnh đáy \(LB =\eqalign {2 \over 3}BC\)

\( \Rightarrow {S_{DLB}} = \eqalign{2 \over 3}{S_{DBC}}\)

mà \({S_{DAC}} = {S_{ADB}} = {S_{DBC}}\) (chứng minh trên)

Suy ra: \({{S_{ADLB}} = {S_{DAC}} + \eqalign{2 \over 3}{S_{DAC}}} \) \({= \eqalign{5 \over 3}{S_{DAC}}} \)

\(\Rightarrow \eqalign{{{S_{DAC}}} \over {{S_{ADLB}}}} = \eqalign{3 \over 5}\)

c) Ta có: \({S_{ABKD}} = {S_{ABD}} + {S_{DKB}}\)

\(∆ DKB\) và \(∆ DCB\) có chung chiều cao kẻ từ \(D,\) cạnh đáy \(BL = \eqalign{1 \over 3}BC\)

\( \Rightarrow {S_{DKB}} = \eqalign{1 \over 3}{S_{DCB}}\)

mà \({S_{DAC}} = {S_{ADB}} = {S_{DBC}}\) (chứng minh trên)

\( \Rightarrow {S_{ABKD}} = {S_{DAC}} + \eqalign{1 \over 3}{S_{DAC}} \) \(=\eqalign {4 \over 3}{S_{DAC}}\)

\(\Rightarrow \eqalign{{{S_{ABKD}}} \over {{S_{ADLB}}}} = \eqalign{{\eqalign{4 \over 3}{S_{DAC}}} \over {\eqalign{5 \over 3}{S_{DAC}}}} = \eqalign{4 \over 5}\)

HocTot.Nam.Name.Vn