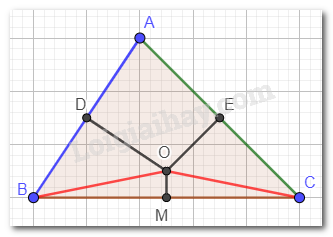
Giải bài 5 trang 115 SGK Toán 7 tập 2 - Cánh diều

Đề bài

Cho tam giác ABC. Đường trung trực của hai cạnh AB và AC cắt nhau tại điểm O nằm trong tam giác. M là trung điểm của BC. Chứng minh:

a) $OM \bot BC$;                                                          

b) $\widehat {MOB} = \widehat {MOC}$.

Lời giải chi tiết

a) Ta có: đường trung trực của hai cạnh AB và AC cắt nhau tại O và O nằm trong tam giác. Nên O là giao điểm của ba đường trung trực của tam giác ABC.

Mà M là trung điểm của cạnh BC nên OM là đường trung trực của đoạn thẳng BC hay $OM \bot BC$.

b) Ta có: Giao của ba đường trung trực trong tam giác thì cách đều ba đỉnh của tam giác đó.

Hay OB = OC nên tam giác OBC cân tại O. Suy ra: $\widehat {OBC} = \widehat {OCB}$ hay $\widehat {OBM} = \widehat {OCM}$. ( tính chất tam giác cân)

Xét tam giác OMB và tam giác OMC có:

     OB = OC;

     $\widehat {OBM} = \widehat {OCM}$;

     MB = MC (M là trung điểm của đoạn thẳng BC).

Vậy $\Delta OMB = \Delta OMC$(c.g.c)

Do đó,$\widehat {MOB} = \widehat {MOC}$ ( 2 góc tương ứng).