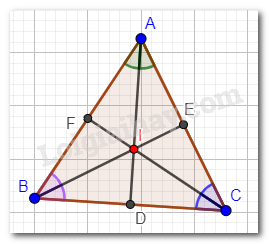
Giải bài 4 trang 115 SGK Toán 7 tập 2 - Cánh diều

Đề bài

Tam giác ABC có ba đường phân giác cắt nhau tại I. Biết rằng I cũng là giao điểm ba đường trung trực của tam giác ABC. Chứng minh tam giác ABC đều.

Lời giải chi tiết

Ta có: I là giao điểm của ba đường phân giác của tam giác ABC. Đồng thời là giao điểm của ba đường trung trực tam giác ABC nên: $ID \bot BC;IE \bot AC;IF \bot AB$.

Xét tam giác ADB và tam giác ADC có:

     $\widehat {BAD} = \widehat {CAD}$(AD là phân giác của góc A);

     AD chung;

     $\widehat {ADB} = \widehat {ADC}(=90^0)$(vì $ID \bot BC$).

Vậy $\Delta ADB = \Delta ADC$(g.c.g). Suy ra: AB = AC ( 2 cạnh tương ứng). (1)

Tương tự ta có: $\Delta BEA = \Delta BEC$(g.c.g). Suy ra: BA = BC ( 2 cạnh tương ứng). (2)

Từ (1) và (2) suy ra: AB = BC = AC.

Vậy tam giác ABC đều.