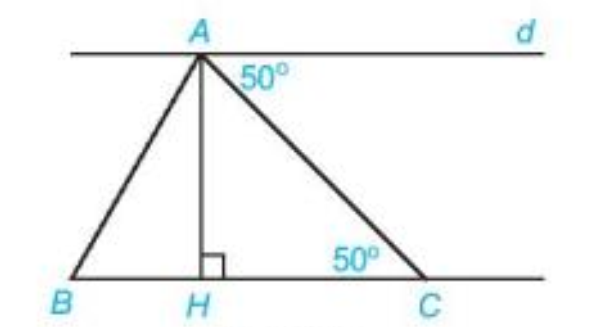
Giải bài 5 (3.31) trang 52 vở thực hành Toán 7Bài 5 (3.31). Cho hình 3.18. Chứng minh rằng: a) d // BC; b) \(d \bot AH\); c) Trong các kết luận trên, kết luận nào được suy ra từ tính chất của hai đường thẳng song song, kết luận nào được suy ra từ dấu hiệu nhận biết hai đường thẳng song song? Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên... Đề bài Bài 5 (3.31). Cho hình 3.18. Chứng minh rằng: a) d // BC; b) \(d \bot AH\); c) Trong các kết luận trên, kết luận nào được suy ra từ tính chất của hai đường thẳng song song, kết luận nào được suy ra từ dấu hiệu nhận biết hai đường thẳng song song?
Phương pháp giải - Xem chi tiết Dấu hiệu nhận biết và tính chất của hai đường thẳng song song Lời giải chi tiết a) Ta có \(\widehat {dAC} = \widehat {ACB} = {50^o}\) mà hai góc này ở vị trí so le trong nên d // BC (dấu hiệu nhận biết hai đường thẳng song song). b) Ta có \(AH \bot BC\) mà d // BC nên \(AH \bot d\) c) Kết luận d // BC được suy ra từ dấu hiệu nhận biết hai đường thẳng song song Kết luận \(AH \bot d\) được suy ra từ tính chất của hai đường thẳng song song.
|