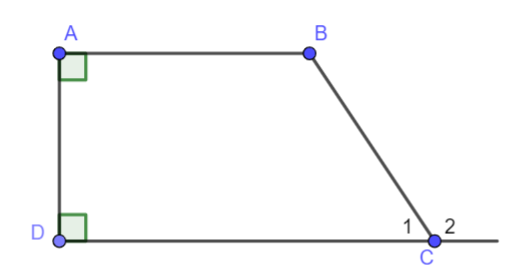
Giải bài 1 (3.27) trang 50 vở thực hành Toán 7Bài 1 (3.27). Cho hình thang ABCD có cạnh AD vuông góc với hai đáy AB và CD. Số đo góc ở đỉnh B gấp đôi số đo góc ở đỉnh C. Tính số đo các góc của hình thang đó. Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên... Đề bài Bài 1 (3.27). Cho hình thang ABCD có cạnh AD vuông góc với hai đáy AB và CD. Số đo góc ở đỉnh B gấp đôi số đo góc ở đỉnh C. Tính số đo các góc của hình thang đó.
Phương pháp giải - Xem chi tiết Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau Một đường thẳng cắt hai đường thẳng song song thì tạo ra các cặp góc so le trong bằng nhau Lời giải chi tiết Vì AD⊥AB,AD⊥CD nên ˆA=ˆD=90o Ta có AB // CD suy ra ˆB=^C2(hai góc so le trong) Mà ^C1+^C2=180onên ^C1+ˆB=180o Mặt khác ˆB=2^C1 nên ^C1+2^C1=180o⇔3^C1=180o⇔^C1=60o Từ đó suy ra ˆB=2^C1=120o.
|