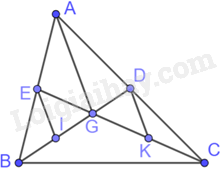
Giải bài 4.9 trang 50 sách bài tập toán 8 - Kết nối tri thức với cuộc sống

Đề bài

Cho tam giác ABC, các đường trung tuyến BD, CE cắt nhau tại G. Gọi I, K theo thứ tự là trung điểm của GB, GC. Chứng minh rằng \(EI = DK\)

Lời giải chi tiết

Vì BD, CE là các đường trung tuyến của tam giác ABC nên D, E lần lượt là trung điểm của AC, AB.

Tam giác ABG có I, E lần lượt là trung điểm của GB, AB nên IE là đường trung bình của tam giác ABG. Do đó, \(EI = \frac{1}{2}AG\) (1)

Tam giác AGC có D, K lần lượt là trung điểm của AC, GC nên DK là đường trung bình của tam giác AGC. Do đó, \(DK = \frac{1}{2}AG\) (2)

Từ (1) và (2) ta có: \(EI = DK\)