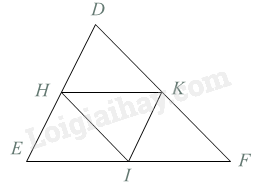
Giải bài 4.8 trang 50 sách bài tập toán 8 - Kết nối tri thức với cuộc sống

Đề bài

Cho tam giác DEF. Gọi H, K, I lần lượt là các trung điểm của DE, DF và EF. Chứng minh rằng tứ giác HKIE là hình bình hành.

Lời giải chi tiết

Tam giác DEF có: H, K lần lượt là trung điểm của DE, DF nên HK là đường trung bình của tam giác DEF. Do đó, HK//EF, $HK = \frac{1}{2}EF$

Mà I là trung điểm của EF nên $EI = \frac{1}{2}EF$

Suy ra: $HK = EI$

Tứ giác HKIE có: $HK//EI (I \in EF), HK = EI$

Do đó, tứ giác HKIE là hình bình hành.