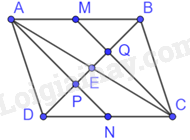
Giải bài 4.6 trang 48 sách bài tập toán 8 - Kết nối tri thức với cuộc sống

Đề bài

Cho hình bình hành ABCD có M, N lần lượt là trung điểm AB và CD. Gọi P, Q theo thứ tự là giao điểm của AN và CM với đường chéo BD. Chứng minh rằng: \(DP = PQ = QB\)

Lời giải chi tiết

Gọi E là giao điểm của AC và BD trong hình bình hành ABCD nên \(DE = BE = \frac{1}{2}BD\), \(AE = EC = \frac{1}{2}AC\)

Tam giác ADC có hai đường trung tuyến AN và DE cắt nhau tại P nên P là trọng tâm của tam giác ADC. Do đó, \(DP = \frac{2}{3}DE = \frac{1}{3}BD\).

Tam giác ABC có hai đường trung tuyến BE và CM cắt nhau tại Q nên Q là trọng tâm của tam giác ABC. Do đó, \(BQ = \frac{2}{3}BE = \frac{1}{3}BD\).

Do đó, \(BQ = DP = \frac{1}{3}BD\)

Mà \(BQ + DP + PQ = BD\) nên \(PQ = \frac{1}{3}BD\)

Vậy \(DP = PQ = QB\)