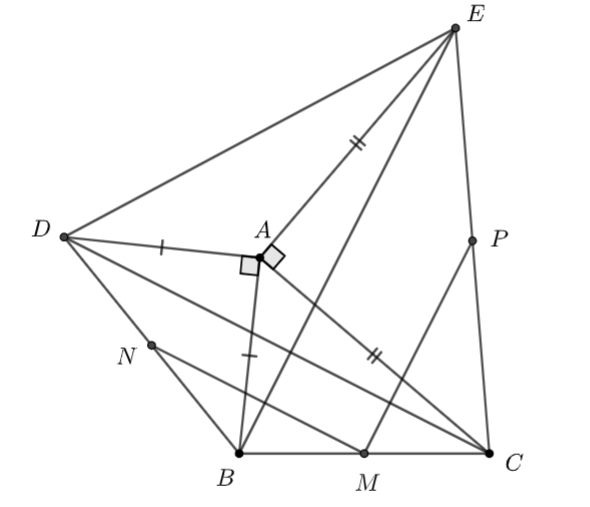
Giải bài 4.31 trang 65 sách bài tập toán 10 - Kết nối tri thức với cuộc sống

Đề bài

Cho tam giác $ABC$ có $\widehat A < {90^ \circ }.$ Dựng ra phía ngoài tam giác hai tam giác vuông cân đỉnh $A$ là $ABD$ và $ACE.$ Gọi $M,\,\,N,\,\,P$ theo thứ tự là trung điểm $BC,\,\,BD,\,\,CE.$ Chứng minh rằng:

a) $AM$ vuông góc với $DE.$

b) $BE$ vuông góc với $CD.$

c) Tam giác $MNP$ là một tam giác vuông cân.

Lời giải chi tiết

a) Ta có: $\overrightarrow {DE}  = \overrightarrow {AE}  - \overrightarrow {AD}$  và  $\overrightarrow {AM}  = \frac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {AC} } \right)$

$\Rightarrow \overrightarrow {AM} .\overrightarrow {DE}  = \frac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {AC} } \right)\left( {\overrightarrow {AE}  - \overrightarrow {AD} } \right)$

 $\begin{array}{l} = \frac{1}{2}\left( {\overrightarrow {AB} .\overrightarrow {AE}  - \overrightarrow {AB} .\overrightarrow {AD}  + \overrightarrow {AC} .\overrightarrow {AE}  - \overrightarrow {AC} .\overrightarrow {AD} } \right)\\ = \frac{1}{2}\left( {\overrightarrow {AB} .\overrightarrow {AE}  - \overrightarrow {AC} .\overrightarrow {AD} } \right)\\ = \frac{1}{2}\left( {AB.AE.\cos \widehat {BAE} - AC.AD.\cos \widehat {CAD}} \right) = 0\end{array}$

$\Rightarrow$ $\overrightarrow {AM}  \bot \overrightarrow {DE}$ $\Rightarrow$ $AM \bot DE$

b) Ta có: $\overrightarrow {BE}  = \overrightarrow {AE}  - \overrightarrow {AB}$ và $\overrightarrow {CD}  = \overrightarrow {AD}  - \overrightarrow {AC}$

$\Rightarrow$ $\overrightarrow {BE} .\overrightarrow {CD}  = \left( {\overrightarrow {AE}  - \overrightarrow {AB} } \right)\left( {\overrightarrow {AD}  - \overrightarrow {AC} } \right)$

$\begin{array}{l} = \overrightarrow {AE} .\overrightarrow {AD}  - \overrightarrow {AE} .\overrightarrow {AC}  - \overrightarrow {AB} .\overrightarrow {AD}  + \overrightarrow {AB} .\overrightarrow {AC} \\ = \overrightarrow {AE} .\overrightarrow {AD}  + \overrightarrow {AB} .\overrightarrow {AC} \\ = AE.AD.\cos \widehat {DAE} + AB.AC.\cos \widehat {BAC}\\ = AE.AD.\cos \widehat {DAE} + AB.AC.\cos \left( {{{180}^ \circ } - \widehat {DAE}} \right) = 0\end{array}$

$\Rightarrow$ $\overrightarrow {BE}  \bot \overrightarrow {CD}$ $\Rightarrow$ $BE \bot CD$

c) Ta có: $MN$ và $MP$ lần lượt là đường trung bình của $\Delta BCD$ và $\Delta ACE$

$\Rightarrow$ $MN$//$CD$ và $MP$//$BE$

mặt khác $CD \bot BE$ (cm câu b)

$\Rightarrow$ $MN \bot MP$

$\Rightarrow$ $\Delta MNP$ vuông tại $M$

+ 

Xét $\Delta ADC$ và $\Delta ABE$ ta có:

$AD = AB$

$AC = AE$

$\widehat {DAC} = \widehat {BAE} = {90^o} + \widehat {BAC}$

$\Rightarrow \Delta ADC = \Delta ABE$ (cạnh góc cạnh)

$\Rightarrow DC = BE$

Lại có: $MN = \frac{1}{2}DC$ (do M, N là trung điểm BD, BC)

$MP = \frac{1}{2}BE$ (do M, N là trung điểm CB, CE)

$\Rightarrow MN = MP$

Vậy tam giác MNP vuông cân tại M.