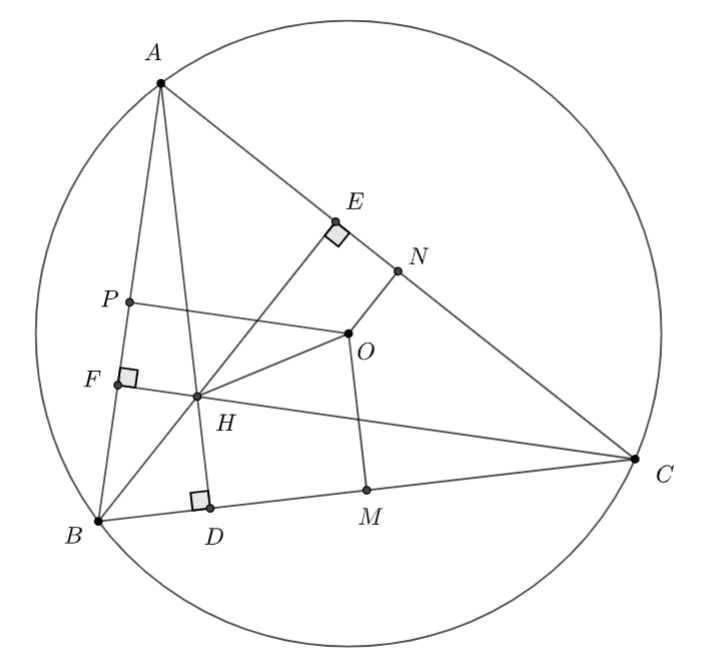
Giải bài 4.33 trang 65 sách bài tập toán 10 - Kết nối tri thức với cuộc sống

Đề bài

Cho tam giác $ABC$ không cân. Gọi $D,\,\,E,\,\,F$ theo thứ tự là chân các đường cao kẻ từ $A,\,\,B,\,\,C;$ gọi $M,\,\,N,\,\,P$ tương ứng là trung điểm các cạnh $BC,\,\,CA,\,\,AB.$ Chứng minh rằng $\overrightarrow {MD} .\overrightarrow {BC}  + \overrightarrow {NE} .\overrightarrow {CA}  + \overrightarrow {PF} .\overrightarrow {AB}  = 0$

Lời giải chi tiết

Gọi $H$ là trực tâm và $O$ là tâm đường tròn ngoại tiếp $\Delta ABC$

Ta có: $ON \bot AC,$ $OM \bot BC,$ $OP \bot AB$ (quan hệ giữa đường kính và dây cung)

Áp dụng định lý chiếu ta có:

$\overrightarrow {MD} .\overrightarrow {BC}  = \overrightarrow {OH} .\left( {\overrightarrow {OC}  - \overrightarrow {OB} } \right) = \overrightarrow {OH} .\overrightarrow {OC}  - \overrightarrow {OH} .\overrightarrow {OB}$     (1)

$\overrightarrow {NE} .\overrightarrow {CA}  = \overrightarrow {OH} .\left( {\overrightarrow {OA}  - \overrightarrow {OC} } \right) = \overrightarrow {OH} .\overrightarrow {OA}  - \overrightarrow {OH} .\overrightarrow {OC}$       (2)

$\overrightarrow {PF} .\overrightarrow {AB}  = \overrightarrow {OH} .\left( {\overrightarrow {OB}  - \overrightarrow {OA} } \right) = \overrightarrow {OH} .\overrightarrow {OB}  - \overrightarrow {OH} .\overrightarrow {OA}$        (3)

Từ (1), (2) và (3) $\Rightarrow$ $\overrightarrow {MD} .\overrightarrow {BC}  + \overrightarrow {NE} .\overrightarrow {CA}  + \overrightarrow {PF} .\overrightarrow {AB}  = 0$ (đpcm)