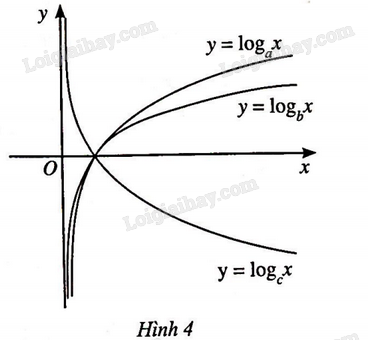
Giải bài 43 trang 45 sách bài tập toán 11 - Cánh diềuCho ba số thực dương \(a,{\rm{ }}b,{\rm{ }}c\) khác 1 Đề bài Cho ba số thực dương \(a,{\rm{ }}b,{\rm{ }}c\) khác 1 và đồ thị của ba hàm số loogarit \(y = {\log _a}x,\)\(y = {\log _b}x\) và \(y = {\log _c}x\) được cho bởi Hình 4. Kết luận nào sau đây là đúng đối với ba số\(a,{\rm{ }}b,{\rm{ }}c?\) A. \(c > b > a.\) B. \(a > b > c.\) C. \(b > a > c.\) D. \(c > a > b.\)
Phương pháp giải - Xem chi tiết - Hàm số lôgarit \(y = {\log _a}x\) với \(0 < a < 1\) nghịch biến trên \(\left( {0; + \infty } \right).\) - Hàm số lôgarit \(y = {\log _a}x\) với \(a > 1\) đồng biến trên \(\left( {0; + \infty } \right).\) Lời giải chi tiết Hàm số lôgarit \(y = {\log _a}x\) và \(y = {\log _b}x\) đồng biến trên \(\left( {0; + \infty } \right) \Rightarrow a > 1;{\rm{ }}b > 1.\) Hàm số lôgarit \(y = {\log _c}x\) nghịch biến trên \(\left( {0; + \infty } \right) \Rightarrow 0 < c < 1.\) Thay \(x = 100 \Rightarrow {\log _a}100 > {\log _b}100 > 0 \Leftrightarrow \frac{1}{{{{\log }_{100}}a}} > \frac{1}{{{{\log }_{100}}b}}\) \( \Leftrightarrow {\log _{100}}b > {\log _{100}}a \Leftrightarrow b > a > 1.\) Vậy \(b > a > c.\) Đáp án C.  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
