Giải bài 4.19 trang 54 sách bài tập toán 10 - Kết nối tri thức với cuộc sống

Đề bài

Cho tam giác $ABC.$

a)      Tìm điểm $M$ sao cho $\overrightarrow {MA}  + \overrightarrow {MB}  + 2\overrightarrow {MC}  = \overrightarrow 0$

b)     Xác định điểm $N$ thỏa mãn $4\overrightarrow {NA}  - 2\overrightarrow {NB}  + \overrightarrow {NC}  = \overrightarrow 0$

Lời giải chi tiết

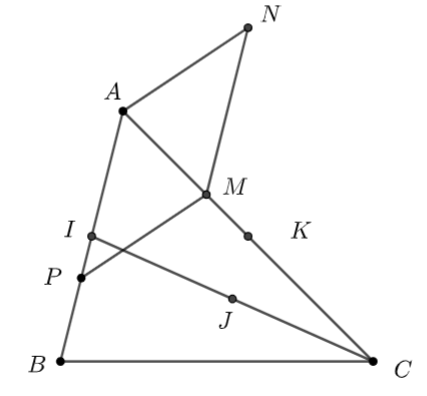
a)      Giả sử tìm được điểm $M$ sao cho $\overrightarrow {MA}  + \overrightarrow {MB}  + 2\overrightarrow {MC}  = \overrightarrow 0$

Gọi $I$ là trung điểm của $AB$ và $J$ là trung điểm của cạnh $CI$.

Ta có: $\overrightarrow {MA}  + \overrightarrow {MB}  + 2\overrightarrow {MC}  = \;\overrightarrow {MI}  + \overrightarrow {IA}  + \overrightarrow {MI}  + \overrightarrow {IB}  + 2\overrightarrow {MC}  = 2\overrightarrow {MI}  + 2\overrightarrow {MC}  = 4\overrightarrow {MJ}$

Mặt khác $\overrightarrow {MA}  + \overrightarrow {MB}  + 2\overrightarrow {MC}  = \overrightarrow 0$

$\Rightarrow$ $4\overrightarrow {MJ}  = \overrightarrow 0 \,\, \Rightarrow \,\,\overrightarrow {MJ}  = \overrightarrow 0 \,\, \Rightarrow \,\,M \equiv J$

Vậy $M$ là trung điểm của $CI$.

b)     Giả sử tìm được điểm $N$ thỏa mãn $4\overrightarrow {NA}  - 2\overrightarrow {NB}  + \overrightarrow {NC}  = \overrightarrow 0$

Gọi $K$ là trung điểm của $AC$.

Ta có: $4\overrightarrow {NA}  - 2\overrightarrow {NB}  + \overrightarrow {NC}  = 2\left( {\overrightarrow {NA}  - \overrightarrow {NB} } \right) + \left( {\overrightarrow {NA}  + \overrightarrow {NC} } \right) + \overrightarrow {NA}$

                                                     $\begin{array}{l} = 2\overrightarrow {BA}  + \left( {\overrightarrow {NK}  + \overrightarrow {KB}  + \overrightarrow {NK}  + \overrightarrow {KC} } \right) + \overrightarrow {NA} \\ = 2\overrightarrow {BA}  + 2\overrightarrow {NK}  + \overrightarrow {NA} \end{array}$

Gọi $M$ là điểm thỏa mãn $2\overrightarrow {MK}  + \overrightarrow {MA}  = 0$

Khi đó: $2\overrightarrow {NK}  + \overrightarrow {NA}  = 2\left( {\overrightarrow {NM}  + \overrightarrow {MK} } \right) + \overrightarrow {NM}  + \overrightarrow {MA}  = 3\overrightarrow {NM}$

Do đó $4\overrightarrow {NA}  - 2\overrightarrow {NB}  + \overrightarrow {NC}  = 2\overrightarrow {BA}  + 3\overrightarrow {NM}$

Mặt khác $4\overrightarrow {NA}  - 2\overrightarrow {NB}  + \overrightarrow {NC}  = \overrightarrow 0$

$\Rightarrow$ $2\overrightarrow {BA}  + 3\overrightarrow {NM}  = \overrightarrow 0$ $\Leftrightarrow$ $\overrightarrow {NM}  = \frac{2}{3}\overrightarrow {AB}$    (1)

Lấy điểm $P$ thuộc cạnh $AB$ sao cho $\overrightarrow {AP}  = \frac{2}{3}\overrightarrow {AB}$    (2)

Từ (1) và (2) $\Rightarrow$ $\overrightarrow {NM}  = \overrightarrow {AP}$

$\Rightarrow$ tứ giác $APMN$ là hình bình hành

Vậy điểm $N$ cần tìm là đỉnh thứ tư của hình bình hành $APMN$.