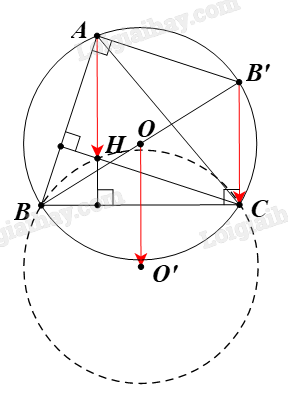
Giải bài 4 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo

Đề bài

Cho hai điểm B, C cố định trên đường tròn $\left( {O;{\rm{ }}R} \right)$ và một điểm A thay đổi trên đường tròn đó. Chứng minh trực tâm H của tam giác ABC luôn nằm trên một đường tròn cố định.

Lời giải chi tiết

Kẻ đường kính BB’.

Do B, C cố định trên (O) nên B’, C cũng cố định trên (O).

Suy ra $\overrightarrow {B'C}$ là vectơ không đổi.

Ta có $\widehat {BCB'} = 90^\circ$ (góc nội tiếp chắn nửa đường tròn (O)).

Suy ra $BC \bot B'C.$

Mà $AH \bot BC$  (do H là trực tâm của ∆ABC).

Do đó $AH//B'C\,\,\left( 1 \right)$

Chứng minh tương tự, ta được $AB'//CH{\rm{ }}\left( 2 \right)$

Từ (1), (2), suy ra tứ giác AHCB’ là hình bình hành.

Suy ra $AH{\rm{ }} = {\rm{ }}B'C.$

Mà $AH{\rm{ }}//{\rm{ }}B'C$  (chứng minh trên).

Vì vậy $\overrightarrow {AH}  = \overrightarrow {B'C}$

Do đó $H = {T_{\overrightarrow {B'C} }}\left( A \right)$.

Vậy khi A thay đổi trên đường tròn (O) thì trực tâm H của tam giác ABC luôn nằm trên ảnh của đường tròn (O) là đường tròn (O’) qua ${{\rm{T}}_{\overrightarrow {B'C} }}$.