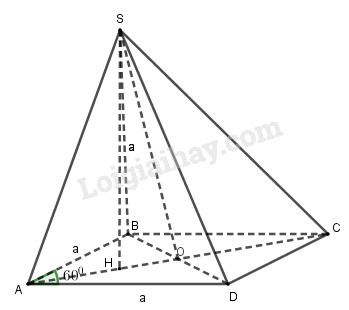
Bài 3.51 trang 163 SBT hình học 11

Đề bài

Cho hình chóp S.ABCD, đáy ABCD là hình thoi cạnh a, ∠BAD = $60^0$, SA = SB = SD = a.

a) Chứng minh (SAC) vuông góc với (ABCD).

b) Chứng minh tam giác SAC vuông.

c) Tính khoảng cách từ S đến (ABCD).

Quảng cáo

Lời giải chi tiết

a) Nhận xét: Tam giác ABD là tam giác đều.

Gọi H là hình chiếu vuông góc của S xuống mặt phẳng (ABD), ta có:

SA = SB = SD ⇒ H là tâm đường tròn ngoại tiếp tam giác ABD

⇒ H là trọng tâm tam giác ABD

⇒ H ∈ AC.

$\Rightarrow SH \subset \left( {SAC} \right)$

Mà $SH \bot \left( {ABCD} \right)$ $\Rightarrow \left( {SAC} \right) \bot \left( {ABCD} \right)$

b) AO là đường cao trong tam giác đều ABD cạnh a nên $AO = \dfrac{{a\sqrt 3 }}{2}$.

$\Rightarrow AH = \dfrac{2}{3}AO$ $= \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}$

$\Rightarrow SH = \sqrt {S{A^2} - A{H^2}}$ $= \sqrt {{a^2} - \dfrac{{{a^2}}}{3}}  = \dfrac{{a\sqrt 6 }}{3}$

Ta có: $HC = AC - AH = 2AO - AH$ $= 2.\dfrac{{a\sqrt 3 }}{2} - \dfrac{{a\sqrt 3 }}{3} = \dfrac{{2a\sqrt 3 }}{3}$

$\Rightarrow SC = \sqrt {S{H^2} + H{C^2}}$ $= \sqrt {\dfrac{{6{a^2}}}{9} + \dfrac{{12{a^2}}}{9}}  = a\sqrt 2$

Tam giác SAC có:

$S{A^2} + S{C^2} = {a^2} + 2{a^2} = 3{a^2}$ và $A{C^2} = {\left( {2AO} \right)^2} = {\left( {2.\dfrac{{a\sqrt 3 }}{2}} \right)^2} = 3{a^2}$

Do đó $S{A^2} + S{C^2} = A{C^2}$ hay tam giác vuông tại S.

c) Ta có: $SH \bot \left( {ABCD} \right)$ $\Rightarrow d\left( {S,\left( {ABCD} \right)} \right) = SH = \dfrac{{a\sqrt 6 }}{3}$

HocTot.Nam.Name.Vn