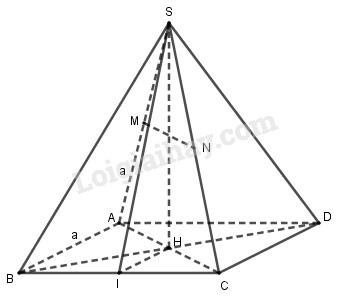
Bài 3.49 trang 163 SBT hình học 11Giải bài 3.49 trang 163 sách bài tập hình học 11. Cho hình chóp tứ giác đều S.ABCD. Gọi M, N lần lượt là trung điểm của SA và SC.... Đề bài Cho hình chóp tứ giác đều S.ABCD. Gọi M, N lần lượt là trung điểm của SA và SC. a) Chứng minh AC ⊥ SD b) Chứng minh MN ⊥ (SBD) c) Cho AB = SA = a. Tính cosin của góc giữa (SBC) và (ABCD) Lời giải chi tiết
a) Gọi H là tâm hình vuông ABCD \( \Rightarrow SH \bot \left( {ABCD} \right)\). Ta có: AC ⊥ SH & AC ⊥ BD ⇒ AC ⊥ (SBD) ⇒ AC ⊥ SD. b) MN là đường trung bình của tam giác SAC nên MN//AC. Mà AC ⊥ (SBD) ⇒ MN ⊥ (SBD). c) + Xác định góc α giữa (SBC) và (ABCD) Gọi I là trung điểm của BC, ta có: BC ⊥ IH & BC ⊥ SH ⇒ BC ⊥ (SIH) ⇒ BC ⊥ SI. Ta có: \(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABCD} \right) = BC\\SI \bot BC\\HI \bot BC\end{array} \right.\) nên góc giữa (SBC) và (ABCD) là góc giữa SI và HI hay \(\widehat {SIH} = \alpha \). + Tính α: Ta có: \(IH = \dfrac{1}{2}AB = \dfrac{a}{2}\) \(SI = \sqrt {S{C^2} - I{C^2}} \) \( = \sqrt {{a^2} - \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 3 }}{2}\) \( \Rightarrow \cos \alpha = \dfrac{{IH}}{{SI}} = \dfrac{a}{2}:\dfrac{{a\sqrt 3 }}{2} = \dfrac{1}{{\sqrt 3 }}\) HocTot.Nam.Name.Vn
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM; 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
|