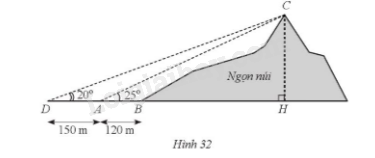
Giải bài 35 trang 91 sách bài tập toán 9 - Cánh diều tập 1Một người (ở vị trí A) dựng cách chân núi (ở vị trí B) là 120 m. Người này đo được góc tạo bởi phương AC và phương nằm ngang là \(\widehat {BAC} = 25^\circ \) với vị trí C là đỉnh núi. Sau đó, người này di chuyển thêm 150 m ra phía xa ngọn núi hơn đến vị trí D) và đo được góc tạo bởi phương DC và phương nằm ngang là \(\widehat {BDC} = 25^\circ \) (Hình 32), Tính chiều cao CH của ngọn núi (làm tròn kết quả đến hàng đơn vị của mét). Đề bài Một người (ở vị trí A) dựng cách chân núi (ở vị trí B) là 120 m. Người này đo được góc tạo bởi phương AC và phương nằm ngang là \(\widehat {BAC} = 25^\circ \) với vị trí C là đỉnh núi. Sau đó, người này di chuyển thêm 150 m ra phía xa ngọn núi hơn đến vị trí D) và đo được góc tạo bởi phương DC và phương nằm ngang là \(\widehat {BDC} = 25^\circ \) (Hình 32), Tính chiều cao CH của ngọn núi (làm tròn kết quả đến hàng đơn vị của mét).
Phương pháp giải - Xem chi tiết Bước 1: Áp dụng tỉ số lượng giác trong tam giác vuông AHC và DHC để tính AH, DH theo CH. Bước 2: Thay AH, DH vào \(AD = DH - AH\) để tính CH. Lời giải chi tiết Xét tam giác AHC vuông tại H, ta có: \(\cot \widehat {CAH} = \frac{{HA}}{{HC}}\) hay \(AH = CH.\cot \widehat {CAH} = CH.\cot 25^\circ \), Xét tam giác DHC vuông tại H, ta có: \(\cot \widehat {CDH} = \frac{{HD}}{{HC}}\) hay \(DH = CH.\cot \widehat {CDH} = CH.\cot 20^\circ \), Mà \(AD = DH - AH\) hay \(CH.\cot 20^\circ - CH.\cot 25^\circ = 150\), do đó \(CH.\left( {\cot 20^\circ - \cot 25^\circ } \right) = 150\). Suy ra \(CH \approx 249\)m. Vậy chiều cao ngọn núi khoảng 249m.  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
