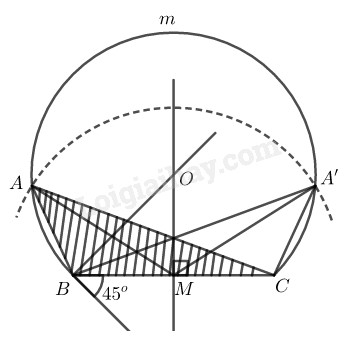
Bài 35 trang 106 SBT toán 9 tập 2

Đề bài

Dựng tam giác \(ABC,\) biết \(BC = 3 cm,\) \(\widehat A = {45^o}\) và trung tuyến \(AM = 2,5 cm.\)

Lời giải chi tiết

Cách dựng:

− Dựng đoạn \(BC = 3cm.\)

− Dựng \(\widehat {CBx} = 45^\circ \)

− Dựng trung điểm \(M\) của \(BC.\)

− Dựng trung trực của \(BC\)

− Dựng tia vuông góc \(Bx\) tại \(B\) cắt đường trung trực của \(BC\) tại \(O.\)

− Dựng cung tròn \(\overparen{BmC}\) bán kính \(OB\) là cung chứa góc \(45^o\) vẽ trên \(BC.\)

− Dựng cung tròn tâm \(M\) bán kính \(2,5 cm\) cắt cung \(\overparen{BmC}\) tại \(A\) và \(A'.\)

− Nối \(AB, AC\) (hoặc \(A’B, A’C\)) ta có \(∆ABC\) (hoặc \(∆A’BC\)) thỏa mãn điều kiện bài toán.

(Chú ý: 

Vì \(BC = 3 cm,\) nên \(MB=MC=BC:2=\dfrac{3}{2}\)

Ta có: \(\widehat {OBM} =90^0-45^0= 45^\circ \) nên tam giác OBM vuông cân tại M.

Nên \(MB=OM=\dfrac{3}{2}\)

Theo định lý Pytago ta có \(OB =\sqrt{MB^2+OM^2}= \displaystyle{{3\sqrt 2 } \over 2}\) \((cm).\)

Khoảng cách \(2\) tâm \(MO = \displaystyle{{3\sqrt 2 } \over 2}\) \((cm)\)

\(\displaystyle{{3\sqrt 2 } \over 2} - 2,5 < MO < {{3\sqrt 2 } \over 2} + 2,5\) nên \((O)\) và \((M)\) luôn cắt nhau. Bài toán luôn dựng được)

Chứng minh: 

 Ta có \(ΔABC\) (hoặc \(ΔA’BC)\) có \(BC = 3cm ,\) góc A \(= 45°\)(hoặc góc \(A'  =45°)\) và trung tuyến \(AM =2,5cm\) (hoặc \(A'M=2,5cm)\) thỏa mãn đề bài.

Biện luận:

Bài toán có hai nghiệm hình.

HocTot.Nam.Name.Vn