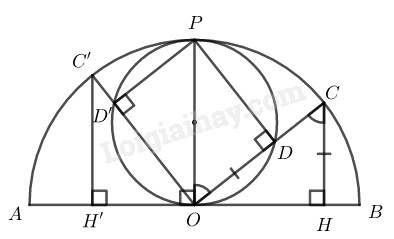
Bài 37 trang 106 SBT toán 9 tập 2Giải bài 37 trang 106 sách bài tập toán 9. Cho nửa đường tròn đường kính AB và C là một điểm trên nửa đường tròn. Trên bán kính OC lấy điểm D sao cho OD bằng khoảng cách CH từ C đến AB. Tìm quỹ tích các điểm D khi C chạy trên nửa đường tròn đã cho. Đề bài Cho nửa đường tròn đường kính \(AB\) và \(C\) là một điểm trên nửa đường tròn. Trên bán kính \(OC\) lấy điểm \(D\) sao cho \(OD\) bằng khoảng cách \(CH\) từ \(C\) đến \(AB.\) Tìm quỹ tích các điểm \(D\) khi \(C\) chạy trên nửa đường tròn đã cho. Phương pháp giải - Xem chi tiết Ta sử dụng kiến thức: +) Với hai cung nhỏ trong một đường tròn, hai dây bằng nhau căng hai cung bằng nhau. Muốn chứng minh quỹ tích (tập hợp) các điểm \(M\) thỏa mãn tính chất \(\tau\) là một hình \({\rm H}\) nào đó, ta phải chứng minh hai phần: Phần thuận: Mọi điểm có tính chất \(\tau\) đều thuộc hình \(\rm H.\) Phần đảo: Mọi điểm thuộc hình \(\rm H\) đều có tính chất \(\tau.\) Kết luận: Quỹ tích (hay tập hợp) các điểm \(M\) có tính chất \(\tau\) là hình \(\rm H.\) Thông thường với bài toán "Tìm quỹ tích..." ta nên dự đoán hình \(\rm H\) trước khi chứng minh: +)Tập hợp các điểm \(M\) tạo với hai mút của đoạn thẳng \(AB\) cho trước một góc \(AMB\) bằng \(\alpha\) \((\alpha\) không đổi \()\) là hai cung tròn đối xứng với nhau qua \(AB\) (gọi là cung chứa góc \(\alpha\) vẽ trên đoạn \(AB\)). +)Quỹ tích các điểm nhìn đoạn thẳng \(AB\) cho trước dưới một góc vuông là đường tròn đường kính \(AB\). Lời giải chi tiết
Chứng minh thuận: Từ \(O\) kẻ đường thẳng vuông góc với \(AB\) cắt nửa đường tròn đường kính \(AB\) tại \(P.\) \(O\) cố định, đường tròn đường kính \(AB\) cố định suy ra \(P\) cố định. Nối \(PD.\) Ta có: \(OP // CH\) (vì hai đường thẳng cùng vuông góc với \(AB\)) Xét \(∆OCH\) và \(∆OPD\) có: +) \(OD = CH (gt)\) +) \(\widehat {POD} = \widehat {OCH}\) (so le trong) +) \(OP = OC\) (bán kính) Suy ra: \(∆DOP = ∆HCO (c.g.c)\) \( \Rightarrow \)\(\widehat {ODP} = \widehat {CHO}\) mà \(\widehat {CHO} = 90^\circ \) nên \(\widehat {ODP} = 90^\circ \) Khi \(C \) chuyển động trên nửa đường tròn đường kính \(AB\) thì \(D\) thay đổi tạo với \(2\) đầu đoạn thẳng \(OP\) cố định một góc \(\widehat {OPD} = 90^\circ \). Vậy \(D\) chuyển động trên đường tròn đường kính \(OP.\) Chứng minh đảo: Lấy điểm \(D'\) bất kỳ trên đường tròn đường kính \(OP.\) Kẻ \(OD'\) cắt nửa đường tròn đường kính \(AB\) tại \(C',\) kẻ \(C'H'⊥ AB\) ta phải chứng minh \(OD' = C'H'.\) Nối \(PD'.\) Xét \(∆C'H'O\) và \(∆PD'O\) có: +) \(\widehat {C'H'O} = \widehat {PD'O} = 90^\circ \) +) \(OC' = OP\) (bán kính đường tròn tâm \(O\)) +) \(\widehat {D'OP} = \widehat {OC'H'}\) (so le trong) Suy ra: \(∆C'H'O = ∆PD'O\) (cạnh huyền, góc nhọn) \( \Rightarrow C'H' = OD'\) Vậy quỹ tích các điểm \(D\) khi \(C\) chuyển động trên nửa đường tròn đường kính \(AB\) là đường tròn đường kính \(OP.\) HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
