Bài 6.2 phần bài tập bổ sung trang 106 SBT toán 9 tập 2Giải bài 6.2 phần bài tập bổ sung trang 106 sách bài tập toán 9. Cho đường tròn tâm O bán kính R và điểm A (khác O) ở trong đường tròn đó. Đề bài Cho đường tròn tâm \(O\) bán kính \(R\) và điểm \(A\) (khác \(O\)) ở trong đường tròn đó. Một đường thẳng \(d\) thay đổi, luôn đi qua \(A,\) cắt đường tròn đã cho tại hai điểm là \(B\) và \(C.\) Tìm quỹ tích trung điểm \(I\) của đoạn thẳng \(BC.\) Phương pháp giải - Xem chi tiết Ta sử dụng kiến thức: Muốn chứng minh quỹ tích (tập hợp) các điểm \(M\) thỏa mãn tính chất \(\tau\) là một hình \({\rm H}\) nào đó, ta phải chứng minh hai phần: Phần thuận: Mọi điểm có tính chất \(\tau\) đều thuộc hình \(\rm H.\) Phần đảo: Mọi điểm thuộc hình \(\rm H\) đều có tính chất \(\tau.\) Kết luận: Quỹ tích (hay tập hợp) các điểm \(M\) có tính chất \(\tau\) là hình \(\rm H.\) Thông thường với bài toán "Tìm quỹ tích..." ta nên dự đoán hình \(\rm H\) trước khi chứng minh: +) Tập hợp các điểm \(M\) tạo với hai mút của đoạn thẳng \(AB\) cho trước một góc \(AMB\) bằng \(\alpha\) \((\alpha\) không đổi \()\) là hai cung tròn đối xứng với nhau qua \(AB\) (gọi là cung chứa góc \(\alpha\) vẽ trên đoạn \(AB\)). +)Quỹ tích các điểm nhìn đoạn thẳng \(AB\) cho trước dưới một góc vuông là đường tròn đường kính \(AB\). Lời giải chi tiết
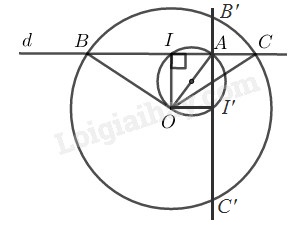
Chứng minh thuận: Đường tròn \((O)\) cho trước, điểm \(A \)cố định nên \(OA\) có độ dài không đổi. \(∆OBC\) cân tại \(O\) (vì \(OB = OC\) = bán kính) \( IB = IC \;\;(gt)\) nên \(OI\) là đường trung tuyến vừa là đường cao \( \Rightarrow OI ⊥ BC\) \( \Rightarrow \widehat {OIA} = 90^\circ \) Đường thẳng \(d\) thay đổi nên \(B, C\) thay đổi thì \(I\) thay đổi tạo với \(2\) đầu đoạn \(OA\) cố định góc \(\widehat {OIA} = 90^\circ \). Vậy \(I\) chuyển động trên đường tròn đường kính \(OA.\) Chứng minh đảo: Lấy điểm \(I’\) bất kỳ trên đường tròn đường kính \(AO.\) Đường thẳng \(AI’\) cắt đường tròn (O) tại \(2\) điểm \(B’\) và \(C’.\) Ta chứng minh: \(I’B = I’C’.\) Trong đường tròn đường kính \(AO\) ta có \(\widehat {OI'A} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow OI'⊥ B'C'\) \( \Rightarrow I'B' = I'C' \) (đường kính vuông góc với dây cung thì đi qua trung điểm dây cung đó) Vậy quỹ tích các điểm \(I\) là trung điểm của dây \(BC\) của đường tròn tâm \(O\) khi \(BC\) quay xung quanh điểm \(A\) cố định là đường tròn đường kính \(AO.\) HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
