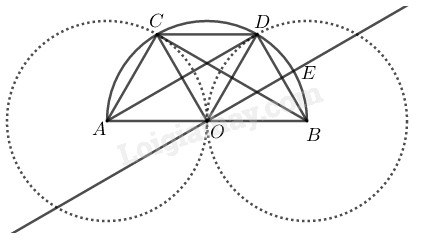
Bài 3.2 phần bài tập bổ sung trang 103 SBT toán 9 tập 2

Đề bài

Cho nửa đường tròn đường kính $AB,$ tâm $O.$ Đường tròn tâm $A$ bán kính $AO$ cắt nửa đường tròn đã cho tại $C.$ Đường tròn tâm $B$ bán kính $BO$ cắt nửa đường tròn đã cho tại $D.$ Đường thẳng qua $O$ và song song với $AD$ cắt nửa đường tròn đã cho tại $E.$

$a)$ $\widehat {ADC}$ và $\widehat {ABC}$ có bằng nhau không$?$ Vì sao$?$

$b)$ Chứng minh $CD$ song song với $AB.$

$c)$ Chứng minh $AD$ vuông góc với $OC$

$d)$ Tính số đo của $\widehat {DAO}$.

$e)$ So sánh hai cung $BE$ và $CD.$

Lời giải chi tiết

$a)$ Trong đường tròn $(O)$ ta có:

$\widehat {ADC} = \widehat {ABC}$  ($2$ góc nội tiếp cùng chắn cung $\overparen{AC}$)

$b)$ $∆ACB$ nội tiếp trong đường tròn $(O)$ có $AB$ là đường kính nên $∆ABC$ vuông tại $C$

$\Rightarrow CO = OA = \displaystyle{1 \over 2}AB$ (tính chất tam giác vuông)

Mà $AC = AO$  (bán kính đường tròn $(A)$)

Suy ra: $AC = AO = OC$

$\Rightarrow$$∆ACO$ đều $\Rightarrow \widehat {AOC} = {60^o}$

Ta có: $∆ADB$ nội tiếp trong đường tròn đường kính $AB$ nên $∆ADB$ vuông tại $D$

$\Rightarrow DO = OB = OA = \displaystyle {1 \over 2}AB$ (tính chất tam giác vuông)

$BD = BO$ (bán kính đường tròn $(B)$)

Suy ra: $BO = OD = BD$

$\Rightarrow$ $∆BOD$ đều

$\Rightarrow \widehat {ODB} = \widehat {BOD} = {60^o}$

Mà $\widehat {AOC} + \widehat {COD} + \widehat {BOD} = {180^o}$

Suy ra: $\widehat {COD} = {60^o}$

Kết hợp với: $OC = OD$  (vì cùng bằng $\displaystyle {1 \over 2}AB$)

Suy ra: $∆COD$ đều

$\Rightarrow \widehat {ODC} = {60^o} \Rightarrow \widehat {ODC} = \widehat {BOD}$

$\Rightarrow$ $CD // AB$ (vì có cặp góc ở vị trí so le trong bằng nhau)

$c)$ Ta có: $∆AOC$ đều (chứng minh trên) $\Rightarrow OA = AC = OC$

$∆OCD$ đều (chứng minh trên)  $\Rightarrow OC = OD = CD$

Suy ra: $AC = AO = OD = DC$

Vậy: tứ giác $AODC$ là hình thoi. Suy ra $AD \bot OC.$

$d)$ $∆BOD$ đều (chứng minh trên) $\Rightarrow \widehat {OBD} = {60^o}$ hay $\widehat {ABD} = {60^o}$

Vì $∆ADB$ vuông tại $D$

$\Rightarrow \widehat {DAB} + \widehat {ABD} = {90^o}$

$\Rightarrow \widehat {DAB} = {90^o} - \widehat {ABD}$$= {90^o} - {60^o} = {30^o}$

Vậy $\widehat {DAO} = {30^o}$

$e)$ $OE // AD\;\; (gt)$

$\Rightarrow \widehat {EOB} = \widehat {DAO} = {30^o}$ (hai góc đồng vị)

$sđ \overparen{BE}$ $= \widehat {EOB} = {30^0}$

$sđ \overparen{CD}$ $= \widehat {COD}$

mà $\widehat {COD} = {60^o}$ (chứng minh trên)

$sđ \overparen{CD} = 60^o$

Suy ra: Số đo cung $\overparen{CD}$ gấp đôi số đo cung $\overparen{BE}$.

HocTot.Nam.Name.Vn