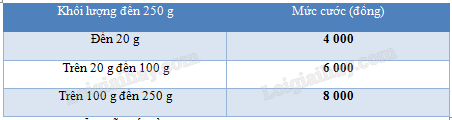
Giải bài 31 trang 81 sách bài tập toán 11 - Cánh diềuTheo quyết định số 2019/QĐ-BĐVN ngày 01/11/2018 của Tổng công ty Bưu điện Việt Nam Tổng hợp đề thi học kì 2 lớp 11 tất cả các môn - Cánh diều Toán - Văn - Anh - Lí - Hóa - Sinh Đề bài Theo quyết định số 2019/QĐ-BĐVN ngày 01/11/2018 của Tổng công ty Bưu điện Việt Nam, giá cước dịch vụ Bưu chính phổ cập đối với dịch vụ thư cơ bản và bưu thiếp trong nước có khối lượng đến 250 g như trong bảng sau:
a) Hãy biểu diễn số tiền phải trả khi sử dụng dịch vụ thư cơ bản và bưu thiếp theo khối lượng của thư cơ bản và bưu thiếp. b) Hàm số trên có liên tục trên tập xác định hay không?
Phương pháp giải - Xem chi tiết a) Dựa vào bảng, ta thấy với khối lượng từ 0 đến 20 g thì mức cước là 4000 đồng, từ trên 20 g đến 100 g thì mức cước là 6000 đồng, từ trên 100 g đến 250 g thì mức cước là 8000 đồng. Từ đó ta sẽ có hàm số biểu diễn số tiền phải trả khi sử dụng dịch vụ thư cơ bản và bưu thiếp theo khối lượng của thư cơ bản và bưu thiếp. b) Hàm số có tập xác định là (0,250]. Sử dụng các tính chất của hàm số liên tục. Lời giải chi tiết a) Dựa vào bảng, ta thấy với khối lượng từ 0 đến 20 g thì mức cước là 4000 đồng, từ trên 20 g đến 100 g thì mức cước là 6000 đồng, từ trên 100 g đến 250 g thì mức cước là 8000 đồng. Như vậy, nếu gọix là khối lượng của thư cơ bản và bưu thiếp và f(x) là số tiền phải trả thì ta có hàm số: f(x)={4000(0<x≤20)6000(20<x≤100)8000(100<x≤250). b) Hàm số có tập xác định là (0,250]. Ta có lim và \mathop {\lim }\limits_{x \to {{20}^ + }} f\left( x \right) = 6000. Do \mathop {\lim }\limits_{x \to {{20}^ - }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {{20}^ + }} f\left( x \right), nên không tồn tại \mathop {\lim }\limits_{x \to 20} f\left( x \right). Suy ra hàm số không liên tục tại x = 20. Mà 20 \in \left( {0,250} \right], ta kết luận hàm số không liên tục trên tập xác định của nó.
|