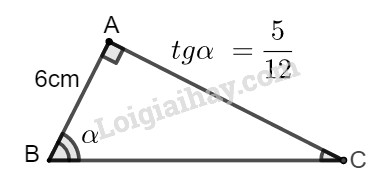
Bài 24 trang 106 SBT toán 9 tập 1Giải bài 24 trang 106 sách bài tập toán 9. Cho tam giác ABC vuông tại A. Đề bài Cho tam giác \(ABC\) vuông tại \(A\), \(AB = 6cm,\widehat B = \alpha \). Biết \(tg\alpha = \dfrac{5}{{12}}.\) Hãy tính: a) Cạnh \(AC\); b) Cạnh \(BC\). Phương pháp giải - Xem chi tiết Các tỉ số lượng giác của góc nhọn (hình) được định nghĩa như sau:
\(\sin \alpha = \dfrac{{AB}}{{BC}};\cos \alpha = \dfrac{{AC}}{{BC}};\)\(\tan \alpha = \dfrac{{AB}}{{AC}};\cot \alpha = \dfrac{{AC}}{{AB}}.\) Định lí Pytago vào tam giác ABC vuông tại A: \(A{B^2} + A{C^2} = B{C^2}.\) Lời giải chi tiết
Giả sử tam giác \(ABC\) có \(\widehat A = 90^\circ ,\widehat B = \alpha .\) a) Ta có: \(\tan\alpha = \tan\widehat B = \dfrac{{AC}}{{AB}}\) Suy ra: \(AC = AB.\tan\widehat B = AB.\tan\alpha \)\( = 6.\dfrac{5}{{12}} = 2,5\left( {cm} \right)\) b) Áp dụng định lí Pytago vào tam giác vuông \(ABC\), ta có: \(B{C^2} = A{B^2} + A{C^2}\)\( = {6^2} + {(2,5)^2} = 42,25\) Suy ra: \(BC = \sqrt {42,25} = 6,5\left( {cm} \right).\)  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
