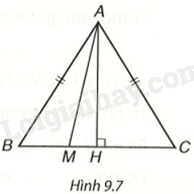
Giải bài 2 (9.8) trang 69, 70 vở thực hành Toán 7 tập 2Cho tam giác cân ABC, (AB = AC). Lấy điểm M tùy ý nằm giữa B và C (H.9.7). a) Khi M thay đổi thì độ dài AM thay đổi. Xác định vị trí của điểm M để độ dài AM nhỏ nhất. b) Chứng minh rằng với mọi điểm M thì (AM < AB). Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên... Đề bài Cho tam giác cân ABC, AB=AC. Lấy điểm M tùy ý nằm giữa B và C (H.9.7).
a) Khi M thay đổi thì độ dài AM thay đổi. Xác định vị trí của điểm M để độ dài AM nhỏ nhất. b) Chứng minh rằng với mọi điểm M thì AM<AB. Phương pháp giải - Xem chi tiết + Trong các đường xiên và đường vuông góc kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường vuông góc là đường ngắn nhất. + Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn. Lời giải chi tiết a) Kẻ đường cao AH của tam giác ABC, ta có AH là đường vuông góc hạ từ điểm A xuống BC. Gọi M là điểm tùy ý nằm giữa B và C. Nếu M khác H thì AM là đường xiên kẻ từ A đến BC. Do đó theo định lí, AH<AM. Vậy AM nhỏ nhất bằng AH khi M trùng H. b) M là một điểm nằm giữa B và C. Ta cần chứng minh AM<AB. Muốn vậy, ta xét các trường hợp sau: Trường hợp 1: Nếu ^AMB=90o, thì AM là đường vuông góc, còn AB là đường xiên kẻ từ A xuống BC theo định lí về đường vuông góc và đường xiên, ta có AM<AB. Trường hợp 2: Nếu ^AMB là góc tù thì trong tam giác AMB, góc AMB lớn nhất nên AM<AB. Trường hợp 3: Nếu ^AMB là góc nhọn thì góc AMC kề bù với nó là góc tù. Trong tam giác AMC, góc AMC là góc lớn nhất. Do đó, AM<AC=AB.
|