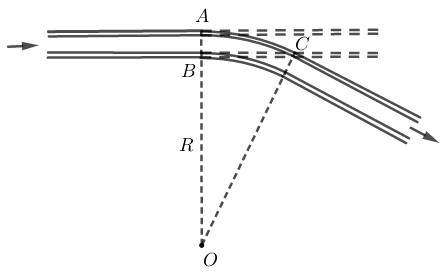
Bài 19 trang 102 SBT toán 9 tập 2Giải bài 19 trang 102 sách bài tập toán 9. Để giúp xe lửa chuyển từ một đường ray từ hướng này sang một đường ray theo hướng khác, người ta làm xen giữa một đoạn đường ray hình vòng cung... Đề bài Để giúp xe lửa chuyển từ một đường ray từ hướng này sang một đường ray theo hướng khác, người ta làm xen giữa một đoạn đường ray hình vòng cung (hình \(1\)). Biết chiều rộng của đường ray là \(AB \approx 1,1m\), đoạn \(BC \approx 28,4m\). Hãy tính bán kính \(OA = R\) của đoạn đường ray hình vòng cung.
Phương pháp giải - Xem chi tiết Ta sử dụng kiến thức: +) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm. +) Đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy. +) Trong một đường tròn, các góc nội tiếp cùng chắn một cung thì bằng nhau. Lời giải chi tiết
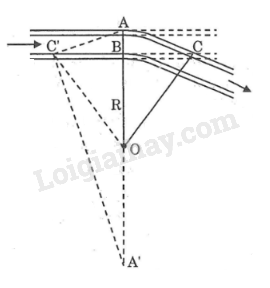
Ta xem hai đoạn đường ray thẳng là tiếp tuyến của hai đoạn đường ray vòng cung. Điểm \(B\) cố định nằm trong đường tròn có cung \(\overparen{AC}\). Đường thẳng \(OB\) cắt đường tròn đó tại \(A\) và \(A’.\) \(A\) cố định và \(A’\) cố định \(B\) là tiếp điểm cung nhỏ trong nên \(BC\) là tiếp tuyến của đường tròn \((O; OB)\) \( \Rightarrow BC \bot OB\). Kéo dài \(BC\) cắt đường tròn \((O; OA)\) tại \(C’\) \( \Rightarrow BC = BC'\) (đường kính vuông góc dây cung) Xét \(∆BAC\) và \(∆BA'C:\) +) \(\widehat {ABC} = \widehat {C'BA'}\) (đối đỉnh) +) \(\widehat {ACB} = \widehat {C'A'B}\) (\(2\) góc nội tiếp cùng chắn cung \(\overparen{AC'}\)) Suy ra: \(∆BAC\) đồng dạng \(∆BC'A' \;\;(g.g)\) \( \Rightarrow \displaystyle {{BC'} \over {AB}} = {{BA'} \over {BC}}\) \( \Rightarrow BC.BC' = AB.BA'\) mà \(BC = BC’; BA’ = 2R – AB\) Suy ra: \(B{C^2} = AB\left( {2R - AB} \right)\) \({\left( {28,4} \right)^2} \approx 1,1.\left( {2R - 1,1} \right)\) \( \Rightarrow 2,2R \approx 806,56 + 1,21\) \(R \approx 807,77:2,2 = 367,2\) \((m).\) HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
